বস্তুপিন্ডগুলির গতি সম্পর্কে আমাদের আধুনিক ধারণার সূত্রপাত গ্যালিলিও এবং নিউটন থেকে। তার আগে লোকে বিশ্বাস করতো অ্যারস্টোটলকে। তিনি বলেছিলেন, বস্তুপিন্ডের স্বাভাবিক অবস্থা স্থিতি এবং সে গতিশীল হয় শুধুমাত্র কোনো বল বা ঘাতের (impulse) দ্বারা। এ মতের ফলশ্রুতি হল একটি হাল্কা বস্তুপিন্ডের তুলনায় একটি ভারী বস্তুপিন্ডের পতন দ্রুততর হবে। তার কারণ পৃথিবীর প্রতি তার আকর্ষণ বেশী।
এ ছাড়াও অ্যারিস্টোটলের ঐতিহ্য বলে, বিশুদ্ধ চিন্তার সাহায্যেই মহাবিশ্ব নিয়ন্ত্রণকারী সমস্ত বিধি (law) গঠন করা সম্ভব। পর্যবেক্ষণের সাহায্যে ব্যাপারটা মিলিয়ে দেখার কোনো প্রয়োজন নেই। সুতরাং, গ্যলিলিওর পূর্ব পর্যন্ত বিভিন্ন ওজনের বস্তুপিন্ডগুলির গতিবেগ বিভিন্ন কিনা- সেটা দেখার জন্য কেউ ব্যস্ত হয় নি। কথিত আছে পিসার হেলানো স্তম্ভ থেকে একাধিক ওজন ফেলে গ্যালিলিও প্রমাণ করেছিলেন অ্যারিস্টোটলের ধারণা ভুল। কাহিনীটা যে অসত্য সেটা প্রায় নিশ্চিত। কিন্তু গ্যালিলিও এই ধরণের একটা কিছু করেছিলেন। তিনি একটি ঢালু মসৃণ পথে বিভিন্ন ওজনের বল গড়িয়ে দিয়েছিলেন। পরিস্থিতিটা ভারী বস্তুপিন্ডের উল্লম্বভাবে (vertically) পতনের মতো। কিন্তু ব্যাপারটা পর্যবেক্ষণ করা সহজতর, তার কারণ গতিবেগ তুলনায় কম। গ্যলিলিওর মাপনে দেখা গেল ওজন যাই হোক না কেন প্রতিটি বস্তুপিণ্ডেরই দ্রুতি (speed) এক রকম। উদাহরণ, একটি বলের ওজন যাই হোক না কেন সেটাকে যদি এখন একটি ঢালু পথে ছেড়ে দেওয়া হয়, যার ঢাল প্রতি দশ মিটারে এক মিটার তা হলে এক সেকেন্ডের পর বলটির দ্রুতি (speed) সেকেন্ডে এক মিটার হবে, দ্বিতীয় সেকেন্ডের পর দ্রুতি হবে প্রতি সেকেন্ডে দুই মিটার এবং এই রকম চলতে থাকবে। অবশ্য একটি সীসক নির্মিত ওজন একটি পালকের চাইতে দ্রুত যাবে। কিন্তু তার একমাত্র কারণ পালকটা বাতাসের বাধা পেয়ে মন্দগতি হয়। কিন্তু যদি এমন দুটি বস্তুপিন্ড নিক্ষেপ করা যায়, যেগুলিকে বাতাস কোন বাধা দেবে না- যথা ভিন্ন ওজনের দুটি সীসক- তা হলে তাদের পতনের হার হবে একই।
গ্যালিলিওর মাপনগুলিকে নিউটন তাঁর গতির বিধির ভিত্তি করেছিলেন (law of motion)। গ্যালিলিওর পরীক্ষাগুলতে একটি বস্তুপিন্ড যখন ঢালু পথে গড়ায়, তখন তার উপরে একই বল (সেটার ওজন) ক্রিয়া করে এবং তার ক্রিয়া হল বস্তুপিন্ডটির অবিচ্ছিন্ন দ্রুতি বৃদ্ধি করা। এ থেকে দেখা গেল একটি বলের বাস্তব ক্রিয়া সব সময়ই অবিচ্ছিন্নভাবে একটি বস্তুপিন্ডের দ্রুতির পরিবর্তন করা। বস্তুপিণ্ডটির গতি শুধু শুরু করাই তার কাজ নয়, যদিও আগে লোকে তাই ভেবেছে। তা ছাড়া এর অর্থ ছিল একটি বস্তুপিন্ডের উপরে যখন একটি বল ক্রিয়া করে বস্তুপিন্ডটি তখন ঋজুরেখায় একই দ্রুতিতে চলতে থাকবে। এই ধারণা প্রথম স্পষ্টভাবে বলা হয় ১৬৮৭ সালে প্রকাশিত নিউটনের প্রিন্সিপিয়া ম্যাথামেটিকাতে (Principia Mathematica)। এটা নিউটনের প্রথম বিধি (law) নামে পরিচিত। একটি বস্তুপিন্ডের উপরে যখন একটি বল ক্রিয়া করে তখন কি হয় সেটা পাওয়া যায় নিউটনের দ্বিতীয় বিধিতে। এই বিধি বলে একটি বস্তুপিন্ডের ত্বরণ কিম্বা তার দ্রুতির হার বলটির সঙ্গে সমানুপাতিক (উদাহরণ; বল যদি দ্বিগুণ হয়, তা হলে ত্বরণও দ্বিগুণ হবে)। বস্তুপিণ্ডটির ভর (mass- পদার্থের পরিমাণ) যত বেশি হবে ত্বরণও তত কম হবে। (একই বল যদি দ্বিগুণ ভরের বস্তুপিন্ডের উপর ক্রিয়া করে তা হলে সে বল অর্ধেক ত্বরণ উৎপাদন করবে।) একটি পরিচিত উদাহরণ হল, আধুনিক মোটর গাড়ি। ইঞ্জিন যত শক্তিশালী হবে, ত্বরণও তত বেশি হবে, কিন্তু গাড়িটার ওজন যদি তুলনায় বেশি হয়, তা হলে ইঞ্জিনটা এক থাকলেও ত্বরণ কম হবে।
গতির বিধি ছাড়াও নিউটন আর একটি বিধি আবিষ্কার করেছিলেন। সে বিধি মহাকর্ষীয় বলের বিবরণ দান করে। এই বিধির বক্তব্য হল, প্রতিটি বস্তুপিন্ডই প্রতিটি অন্য বস্তুপিন্ডকে আকর্ষণ করে। এই আকর্ষণ বল প্রতিটি বস্তুপিন্ডের ভরের সমানুপাতিক। সুতরাং যদি বস্তুপিন্ডগুলির একটির (ধরা যাক, বস্তুপিন্ডটি ক) ভর দ্বিগুণিত করা যায়, তা হলে তাদের অন্তর্বর্তী বলও দ্বিগুণ শক্তিশালী হবে। এটাই আশা করা উচিত, কারণ, নতুন বস্তুপিন্ডকে ভাবা যেতে পারে আগেকার ভর সম্পন্ন দুটি বস্তুপিন্ড। প্রতিটি বস্তুপিন্ড খ বস্তুপিন্ডকে আকর্ষণ করবে আগেকার (original) বলে। সুতরাং ক এবং খ- এর অন্তর্বর্তী মোট বল হবে প্রথম বলের দ্বিগুণ। কিন্তু ধরুন একটি বস্তুপিন্ডের ভর যদি দ্বিগুণ হয় এবং আর একটি বস্তুপিন্ডের ভর যদি তিনগুণ হয়, তা হলে বল হবে ছয় গুণ শক্তিশালী। এখন বোঝা যায় কেন সমস্ত বস্তুপিন্ডগুলির পতনের হার এক। কিন্তু তার ভরও দ্বিগুণ হবে। নিউটনের দ্বিতীয় বিধি (law) অনুসারে এই দুটি ক্রিয়া পরস্পরকে নির্ভুলভাবে বাতিল করবে। সুতরাং সর্বক্ষেত্রে ত্বরণ এক থাকবে।
নিউটনের মহাকর্ষীয় বিধি আরো বলে যে, বস্তুপিন্ডগুলির দূরত্ব যত বেশি হবে বলও তত কম হবে। নিউটনের মহাকর্ষীয় বিধি অনুসারে একটি তারকার মহাকর্ষীয় আকর্ষণ, অর্ধেক দূরত্বে অবস্থিত একই রকম আর একটি তারকার আকর্ষণের তুলনায় এক চতুর্থাংশ হবে। এই বিধি পৃথিবী, চন্দ্র এবং বিভিন্ন গ্রহের কক্ষ (orbit) সম্পর্কে অত্যন্ত নির্ভুল ভবিষ্যদ্বাণী করে। বিধি যদি এমন হতো যে একটি তারকার দূরত্বের সঙ্গে আকর্ষণ আরো দ্রুত হ্রাস পায় তা হলে গ্রহগুলির কক্ষ (orbit) উপবৃত্তাকার (elliptical) না হয়ে সেগুলির পথ হতো সর্পিল এবং তারা সূর্যে পতিত হত। এগুলির হ্রাসপ্রাপ্তি যদি মন্দতর হত, তা হলে সুদূরে অবস্থিত তারকাগুলির মহাকর্ষীয় বল পৃথিবীর মহাকর্ষীয় বলের উপর আধিপত্য করত।
অ্যারিস্টোটলীয় ধারণা এবং নিউটন গ্যালিলিওর ধারণার ভিতরে বড় পার্থক্য হল, অ্যারিস্টোটলের মতে বস্তুপিন্ডগুলির স্থিতাবস্থাই পছন্দ। তাঁর মতে যে কোন বস্তুপিন্ডই স্থিতাবস্থায় থাকবে অবশ্য যদি কোন বল কিম্বা ঘাত তার উপর ক্রিয়া না করে। বিশেষ করে তিনি ভাবতেন পৃথিবীটা স্থিতিশীল। কিন্তু নিউটনের বিধির ফলশ্রুতি হল, স্থিতির কোন অনন্য (unique) মান নেই। বলা যেতে পারে বস্তুপিন্ড ক স্থিতিশীল এবং বস্তুপিন্ড খ বস্তুপিন্ড ক সাপেক্ষ একটা স্থির দ্রুতি চলমান। কিম্বা বলা যেতে পারে বস্তুপিন্ড খ স্থিথিশীল এবং বস্তুপিন্ড ক চলমান। দুটি বিবৃতিই সমভাবে প্রযোজ্য। উদাহরণ, যদি মুহূর্তের জন্য- পৃথিবীর আবর্তন এবং সূর্যকে ঘিরে তার কক্ষ (orbit) না বিচার করা যায়, তা হলে বলা যেতে পারে পৃথিবী স্থিতিশীল এবং একটি রেলগাড়ি তার উপরে ঘণ্টায় নব্বই মাইল বেগে উত্তরমুখী চলেছেকিম্বা বলা যেতে পারে ট্রেনটা স্থিথিশীল এবং পৃথিবী ঘণ্টায় নব্বই মাইল বেগে দক্ষিন দিকে চলেছেও। গাড়িটির ভিতরে যদি কেউ গতিশীল বস্তুপিন্ড নিয়ে পরীক্ষা নিরীক্ষা করেন, তা হলে দেখবেন নিউটনের বিধিগুলি সেক্ষেত্রেও সত্য। উদাহরণঃ রেলগাড়িতে যদি কেউ পিং পং খেলেন, তাহলে দেখবেন নিউটনীয় বিধি মেনে চলছে। রেললাইনের পাশে অবস্থিত একটি টেবিলের উপর যে রকম হয় ঠিক সেই রকম। সুতরাং, রেলগাড়িটি চলমান না পৃথিবী চলমান সেটা বলার কোনো উপায় নেই।
স্থিতির পরম মানের (absolute standard) অর্থঃ দুটি ঘটন যদি বিভিন্ন কালে ঘটে থাকে তাহলে সে দুটি ঘটনার স্থানিক অবস্থান অভিন্ন কিনা সেটা নির্ধারণ করা যায় না। উদাহরণঃ ধরুন আমাদের ট্রেনের ভিতরকার পিং পং বলটা উপর নিচে লাফিয়ে এক সেকেন্ড পর পর টেবিলের একই বিন্দুতে দুবার ঠোকর খেল। রেলরাস্তার উপর যদি কেউ থাকেন তবে তাঁর মনে হবে বলের দুটি ঠোকর হয়েছে চল্লিশ মিটার ব্যবধানে। তার কারণ, দুটি ঠোক্করের মধ্যবর্তী সময়ে ট্রেনটা অতটা দূরত্ব অতিক্রম করত। সুতরাং পরম স্থিতির অনস্তিত্বের অর্থ ছিল একটি ঘটনার স্থানে পরম অবস্থান কারও পক্ষে বলা সম্ভব ছিল না। অ্যারিস্টোটল কিন্তু ভেবেছিলেন এটা সম্ভব। ট্রেনের একজন লোক সাপেক্ষ এবং রেলরাস্তার উপরের একজন লোক সাপেক্ষে ঘটনাগুলির অবস্থান এবং তার দূরত্ব ভিন্ন ভিন্ন হবে এবং এক জনের অবস্থানের ফলে অন্য জনের অবস্থান পছন্দ করার কোনো কারণ থাকবে না।
পরম অবস্থান কিম্বা যাকে বলা হয় পরম স্থান- তার এই অনস্তিত্বের জন্য নিউটন খুব উৎকণ্ঠিত হয়েছিলেন। তার কারণ তাঁর পরম ঈশ্বর সম্পর্কীয় ধারণার সঙ্গে এ তথ্যের মিল ছিল না। এমন কি তিনি পরম স্থানের অনস্তিত্ব মেনে নিতে অস্বীকার করেছিলেন, অথচ তাঁর বিধিগুলির ভিতরে এ তথ্য নিহিত ছিল। এই অযৌক্তিক বিশ্বাসের জন্য অনেকেই তাঁর অত্যন্ত বিরূপ সমালোচনা করেছিলেন। তাঁদের ভিতরে উল্লেখযোগ্য ছিলেন বিশপ বার্কলে (Bishop Berkeley) নামক একজন দার্শনিক। বার্কলের বিশ্বাস ছিল সমস্ত বাস্তব পদার্থ এবং স্থান ও কাল ভ্রমাত্মক (illusion) । বার্কলের মতামত যখন বিখ্যাত ডঃ জনসনকে বলা হয়, তখন তিনি পায়ের অগ্রভাগ দিয়ে একটা বড় পাথরে আঘাত করে বলেছিলেন, “এই মতকে আমি এইভাবেই খন্ডন করি।“
অ্যারস্টোটল এবং নিউটন দুজনেই পরম কালে (absolute time) বিশ্বাস করতেন। অর্থাৎ তাঁদের বিশ্বাস ছিল, দুটি ঘটনার অন্তর্বর্তী কাল নিশ্চিতভাবে মাপা সম্ভব; মাপনক্রিয়া যেই করুন না কেন কাল একই থাকবে। অবশ্য যদি তাঁরা একটি ভাল ঘড়ি ব্যবহার করেন। কাল ছিল স্থান থেকে সম্পূর্ণ পৃথক ও স্থাননিরপেক্ষ এবং অধিকাংশ লোকই ভাবেন এই দৃষ্টিভঙ্গি সাধারণ বুদ্ধিসম্মত। কিন্তু আমাদের স্থান ও কাল সম্পর্কিত ধারণা বদলাতে হয়েছে। আপেল কিম্বা যে সমস্ত গ্রহ তুলনায় ধীরগামী সেগুলির ক্ষেত্রে আমাদের আপাতদৃষ্ট সাধারণ বুদ্ধিজান ধারণায় কাজ হয়। কিন্তু আলোকের দ্রুতি কিম্বা তার কাছাকাছি দ্রুতির ক্ষেত্রে এ সমস্ত ধারণায় কোনো কাজই হয় না।
আলোক সীমিত কিন্তু অত্যন্ত দ্রুত গতিতে চলাচল করে। ১৯৭৬ খৃষ্টাব্দে এই তথ্য আবিষ্কার করেছিলেন ডেনমার্কের জ্যোতির্বিজ্ঞানী ওলে ক্রিস্টেনসেন রোমার (Ole Christensen Roemer)। তিনি পর্যবেক্ষণ করেছিলেন, বৃহস্পতির চাঁদগুলি যখন তার পিছনে যাচ্ছে বলে মনে হয় তাদের তখনকার অন্তর্বর্তী সময়গুলি সঠিক সমান নয়। অর্থাৎ চাঁদগুলির যদি বৃহস্পতিকে প্রদক্ষিণ করার গতির হার স্থির হত তা হলে যা হওয়া উচিত ছিল তা নয়। পৃথিবী এবং বৃহস্পতি সূর্য প্রদক্ষিণের সময় গ্রহ দুটির পারস্পারিক দূরত্বের পরিবর্তন হয়। রোমার লক্ষ্য করেছিলেন, বৃহস্পতি যত দূরে থাকে, তার চাঁদগুলির গ্রহণও তত দেরিতেদ এখা যায়। তাঁর যুক্তি ছিল, এর কারণ- আমরা যখন দূরে অবস্থান করি তখন বৃহস্পতির চাঁদগুলি থেকে আলোক আমাদের কাছে পৌঁছাতে বেশি সময় লাগে। পৃথিবী থেকে বৃহস্পতির দূরত্বের হ্রাস বৃদ্ধি সম্পর্কে তাঁর মাপন কিন্তু খুব বেশি নির্ভুল হয়নি। তাঁর হিসাবে আলোকের দ্রুতি ছিল সেকেন্ডে এক লক্ষ চল্লিশ হাজার মাইল। এর সঙ্গে আধুনিক মান- সেকেন্ডে এক লক্ষ্য ছিয়াশি হাজার মাইলের তুলনা করা যায়। তবুও শুধুমাত্র আলোক সীমিত দ্রুতিতে চলাচল করে এই তথ্য প্রমাণ করাতেই নয়, সেই দ্রুতি মাপনেও রোমারের কৃতিত্ব খুবই উল্লেখযোগ্য। কারণ, নিউটনের প্রিন্সিপিয়া ম্যাথামেটিকা প্রকাশের এগারো বছর আগে তিনি এ আবিষ্কার করেছিলেন।
আলোক বিস্তার সম্পর্কে সঠিক তত্ত্ব ১৮৬৫ সালের পূর্বে আবিষ্কৃত হয় নি। সেই সময় ব্রিটিশ পদার্থবিদ জেমস ক্লার্ক ম্যাক্সওয়েল (James Clerk Maxwell) বিদ্যুৎ এবং চুম্বক সম্পর্কীয় সেই কাল পর্যন্ত প্রচলিত আংশিক তত্ত্বগুলিকে ঐক্যবদ্ধ করতে সমর্থ হন। ম্যাক্সওয়েলের (Maxwell) সমীকরণগুলিকে ঐক্যবদ্ধ করতে সমর্থ হন। ম্যাক্সওয়েলের সমীকরণগুলি ভবিষ্যদ্বাণী করেছিল, সম্মিলিত চুম্বক বিদ্যুতীয় ক্ষেত্রে তরঙ্গের মতো একটি চাঞ্চল্য হওয়া সম্ভব এবং সরোবরের তরঙ্গের মতো সেগুলি স্থির দ্রুতিতে চলমান হবে। এই তরঙ্গগুলির তরঙ্গদৈর্ঘ্য (একটি তরঙ্গশীর্ষ থেকে পরবর্তী তরঙ্গশীর্ষের দূরত্ব) যদি এক মিটার লম্বা তার চাইতে বেশি হয় তাহলে আমরা এখন যাকে বেতার তরঙ্গ বলি তার সঙ্গে সেগুলি অভিন্ন। ক্ষুদ্রতর তরঙ্গদৈর্ঘ্যগুলির নাম মাইক্রোওয়েভ (কয়েক সেন্টিমিটার) কিম্বা অবলোহিত (infrared), এক সেন্টিমিটারের দশ হাজার হাজার ভাগের এক ভাগের চাইতে বেশি)। দৃশ্যমান আলোকের তরঙ্গদৈর্ঘ্য এক সেন্টিমিটারের চল্লিশ মিলিয়ন ভাগ থেকে ৮০ মিলিয়ন ভাগের মাঝামাঝি। এর চাইতে ক্ষুদ্রতর তরঙ্গদৈর্ঘ্যগুলির নাম অতিবেগুনী (ultraviolet), রঞ্জন রশ্মি (X-rays) এবং গামা রশ্মি (gamma rays)।
ম্যাক্সওয়েলের তত্ত্ব ভবিষ্যদ্বাণী করেছিল, রেডিও কিম্বা আলোক তরঙ্গগুলি একটি বিশেষ স্থির দ্রুতিতে চলমান। কিন্তু নিউটনীয় তত্ত্ব পরম স্থিতির ধারণা থকে মুক্ত হয়েছিল। তা হলে যদি অনুমান করা যায়, আলোক একটি স্থির দ্রুতিতে চলাচল করে তাহলে বলতে হবে সেই স্থিরত্বের মাপন কি সাপেক্ষ হবে। সুতরাং অনুমান করা হল ‘ইথার’ বলে একটি পদার্থ আছে, সেই পদার্থ সর্বত্র বিরাজমান- এমন কি বিরাজমান ‘শূন্য’ স্থানেও। শব্দ তরঙ্গ যেরকম বায়ুর ভিতর দিয়ে চলাচল করে, আলোক তরঙ্গেরও সেই একই রকম ইথারের ভিতর দিয়ে চলাচল করা উচিত। সুতরাং তাদের দ্রুতি হওয়া উচিত ইথার সাপেক্ষ। ইথার সাপেক্ষ চলমান বিভিন্ন পর্যবেক্ষকের মনে হবে আলোক তাদের কাছে ভিন্ন ভিন্ন গতিতে আসছে। কিন্তু ইথার সাপেক্ষ আলোকের দ্রুতি স্থির থাকবে। বিশেষ করে, পৃথিবী যখন ইথারের ভিতর দিয়ে সূর্য প্রদক্ষিণ করার পথে, তখন ইথারের ভিতর দিয়ে পৃথিবীর গতির অভিমুখে আলোকের দ্রুতি মাপলে (যখন আমরা আলোকের উৎসের অভিমুখে চলেছি) সেটা গতির সমকোণে আলোকের দ্রুতির (speed) চাইতে উচ্চতর হবে (যখন আমরা উৎসের অভিমুখে যাচ্ছি না)। ১৮৮৭ সালে আলবার্ট মিচেলসন (Albert Michelson) (পরবর্তীকালে তিনিই প্রথম আমেরিকান যিনি পদার্থবিদ্যায় নোবেল প্রাইজ পেয়েছিলেন) এবং এডওয়ার্ড মর্লি (Edward Morley) ক্লীভল্যান্ডের ফলিত বিজ্ঞানের কেস স্কুলে (Case School of Applied Science) অতি যত্নে একটি পরীক্ষা করেন। তাঁরা পৃথিবীর গতির অভিমুখে আলোকের দ্রুতির সঙ্গে পৃথিবীর গতির অভিমুখের সমকোণে আলোকের দ্রুতি তুলনা করেন। তাঁরা বিস্ময়ের সঙ্গে দেখলেন, দুটি দ্রুতিই নির্ভুলভাবে অভিন্ন।
১৮৮৭ সাল থেকে ১৯০৫ সাল পর্যন্ত মিচেলসন মর্লি পরীক্ষা ব্যাখ্যা করার চেষ্টা করা হয়। বস্তুপিন্ডগুলি ইথারের ভিতর দিয়ে চলমান অবস্থায় সংকুচিত হয় এবং ঘড়ি ধীরতর (slower) হয়- এই ভিত্তিতে মিচেলসন মর্লি পরীক্ষার ব্যাখ্যা করার অনেকগুলি চেষ্টা হয়। যারা চেষ্টা করে তাঁদের ভিতরে উল্লেখযোগ্য ছিলেন ওলন্দাজ পদার্থবিদ হেনড্রিক লোরেঞ্জ (Hendrik Lorentz)। কিন্তু সুইজারল্যান্ডের পেটেন্ট অফিসের একজন অখ্যাত কেরানী ১৯০৫ সালে প্রকাশিত একটি বিখ্যাত গবেষণাপত্রে দেখিয়ে দেন পরম কালের ধারণা পরিত্যাগ করলে ইথার সম্পর্কিত সমস্ত ধারণাই অপ্রয়োজনীয় হয়ে যায়। এই অখ্যাত কেরানীর নাম আলবার্ট আইনস্টাইন। কয়েক সপ্তাহ বাদে ফরাসী গণিতবিদ হেনরি পয়েনকেয়ার (Henri Poincare) একই রকম কথা বলেন। আইনস্টাইনের যুক্তিগুলি ছিল পয়েনকেয়ারের যুক্তির তুলনায় পদার্থবিদ্যার নিকটতর। পয়েনকেয়ারের মত ছিল সমস্যাটা গাণিতিক। সাধারণত নতুন তত্ত্বের কৃতিত্ব আইনস্টাইনকে দেওয়া হয় কিন্তু একটি গুরুত্বপূর্ণ অংশের সঙ্গে পয়েনকেয়ারের নাম জড়িয়ে তাঁকে স্মরণ করা হয়।
সে সময় যাকে আপেক্ষিক তত্ত্ব বলা হত তার মূলগত স্বীকার্য ছিল (fundamental postulate) অবাধে চলমান সমস্ত বস্তুপিন্ড সাপেক্ষেই বৈজ্ঞানিক বিধিগুলি এক হতে হবে এবং সেটা হতে হবে বস্তুপিন্ডের দ্রুতি নিরপেক্ষ। এই স্বীকার্য নিউটনের গতি বিষয়ক তত্ত্ব সম্পর্কে সত্য ছিল। কিন্তু এখন এই স্বীকার্য ম্যাক্সওয়েল তত্ত্ব এবং আলোকের গতির ক্ষেত্রে বিস্তার লাভ করল। তাঁরা নিজেরা যত দ্রুতিতেই চলমান হোন না কেন আলোর দ্রুতির মাপন সমস্ত পর্যবেক্ষক সাপেক্ষ একই হবে। এই সরল চিন্তাধারার কতগুলি উল্লেখযোগ্য ফলশ্রুতি রয়েছে। তার ভিতর সবচাইতে পরিচিত হল ভর এবং শক্তির সমতুল্যতা (equivalence)। এ তত্ত্বের সারসংক্ষেপ রয়েছে আইনস্টাইনের বিখ্যাত সমীকরণ E = mc2 –এ। এক্ষেত্রে E = শক্তি, m = ভর এবং c = আলোকের দ্রুতি এবং এই বিধিঃ আলোকের দ্রুতির অর্ধেক কোন গতি হতে পারে না। শক্তি এবং ভরের সমতুল্যতা থাকার ফলে একটি বস্তুপিন্ডের গতির দরুন তার যে শক্তি রয়েছে সে শক্তি তার ভরে যুক্ত হবে। অন্য কথায় বলা যায় তার দ্রুতি বাড়ানো কঠিনতর হবে। যে সমস্ত বস্তুপিন্ডের দ্রুতি আলোকের দ্রুতির কাছাকাছি, আসলে শুধুমাত্র সেই সমস্ত বস্তুপিন্ডের ক্ষেত্রেই এই অভিক্রিয়ার গুরুত্ব রয়েছে। উদাহরণ, বস্তুপিন্ডের দ্রুতি যদি আলোকের দ্রুতির ১০ শতাংশ হয়, তাহলে তার ভর বৃদ্ধি পাবে স্বাভাবিকের চাইতে শতকরা ০.৫ ভাগ মাত্র। কিন্তু তার দ্রুতি আলোকের দ্রুতির ৯০ শতাংশ হলে তার ভর হবে স্বাভাবিক ভরের দ্বিগুণেরও বেশি। বস্তুপিন্ডের দ্রুতি আলোকের দ্রুতির যত নিকটতর হয়, তার ভরও ততই আরো বেশি তাড়াতাড়ি বাড়ে। সুতরাং তার দ্রুতি বাড়াতে আরো বেশি বেশি শক্তির প্রয়োজন হয়। আসলে বস্তুপিন্ডের দ্রুতি কখনোই আলোকের দ্রুতির সমান হতে পারে না। কারণ তাহলে তার ভর হবে অসীম। আর ভর এবং শক্তির সমতুল্যতার তত্ত্ব অনুসারে ঐ অবস্থায় পৌঁছাতে হলে তার প্রয়োজন হবে অসীম শক্তি। সেইজন্য স্বাভাবিক বস্তুপিন্ডের গতি অপেক্ষবাদ দ্বারা আলোর গতির চাইতে নিম্নগতিতে চিরকালের জন্য সীমাবদ্ধ। শুধুমাত্র আলোক কিম্বা অন্য যে কোন তরঙ্গের কোনো ভর নেই তারাই আলোকের দ্রুতিতে চলতে পারে।
অপেক্ষবাদের একই রকম উল্লেখযোগ্য ফলশ্রুতি হল স্থান এবং কাল সম্পর্কে আমাদের চিন্তাধারায় বিপ্লব। নিউটনের তত্ত্ব অনুসারে একটি স্থান থেকে অন্য একটি স্থানে যদি আলোকের একটি স্পন্দন (pulse) প্রেরণ করা যায় তাহলে বিভিন্ন পর্যবেক্ষক সাপেক্ষ তার ভ্রমণকাল সম্পর্কে মতৈক্য হবে (কারণ কাল পরম)। কিন্তু আলোক কতদূর গমন করেছে, সে বিষয়ে সব সময় মতৈক্য হবে না (কারণ স্থান পরম নয়)। যেহেতু, আলোকের দ্রুতি শুধুমাত্র আলোক যে দূরত্ব অতিক্রম করেছে, তার সঙ্গে দূরত্ব অতিক্রম করতে যে কাল ব্যয় হয়েছে, তার ভাগফল। সুতরাং বিভিন্ন প্রযবেক্ষকদের ক্ষেত্রে আলোকের গতিবেগের মাপনে পার্থক্য হয়। অথচ অপেক্ষবাদ অনুসারে সমস্ত পর্যবেক্ষকের ক্ষেত্রেই আলোকের চলনের দ্রুতি সম্পর্কে মতৈক্য হবে। তবুও কিন্তু আলোক কতটা দূরত্ব ভ্রমণ করেছে, সে সম্পর্কে মতৈক্য হবে না সুতরাং যে কাল ব্যয় হয়েছে সে সম্পর্কেও মতৈক্য হবে। (যে কাল ব্যয় হয়েছে সেটা হবে আলোক যে দূরত্ব অতিক্রম করেছে তাঁকে আলোকের দ্রুতি দিয়ে ভাগ করলে যে ভাগফল হয় সেই ভাগফল। দূরত্ব সম্পর্কে পর্যবেক্ষকদের মতৈক্য হবে না। তবে আলোকের দ্রুতি সম্পর্কে তাঁদের মতৈক্য হবে)। অন্যকথায় অপেক্ষবাদ পরম কাল সম্পর্কীয় ধারণাকে শেষ করেছে। দেখা গিয়েছে প্রতিটি পর্যবেক্ষকের অবশ্যই কালের নিজস্ব মাপন থাকতে হবে। যে ঘড়ি বহন করছে সেই ঘড়িটাই সেই কাল নির্দেশ করবে। বিভিন্ন পর্যবেক্ষকেরা সমরূপ ঘড়ি বহন করলেও তাঁরা যে কাল সম্পর্কে একমত হবেন তার কোনো নিশ্চয়তা নেই।
প্রতিটই পর্যবেক্ষকই একটি আলোক কিম্বা বেতার তরঙ্গের স্পন্দন পাঠিয়ে ঘটনাটি কোথায় এবং কখন ঘটেছে সেটা বলবার জন্য রাডার যন্ত্র ব্যবহার করতে পারেন। স্পন্দনের একটি অংশ ঘটনায় (at the event) প্রতিফলিত হয়ে ফিরে আসে এবং পর্যবেক্ষক প্রতিফলনটি ফিরে আসবার কাল মাপেন। তা হলে স্পন্দনটি যখন পাঠানো হয়েছিল এবং প্রতিফলনটি যখন ফিরে এল সেই কালের অর্ধেক হবে ঘটনার কালঃ ঘটনার দূরত্ব হবে চলাচলের কালের অর্ধেককে আলোকের দ্রুতি দিয়ে গুণ করলে যা হয় তাই। (এই অর্থে একটি ঘটনা হল এমন কিছু যা স্থানে একটি বিন্দুতে এবং কালের একটা বিশিষ্ট বিন্দুতে ঘটে।) এই ধারণা (idea) দেখানো হয়েছে চিত্র ২.১ (পৃষ্ঠা ৪০)- এ। স্থান-কাল চিত্রের এটা একটা উদাহরণ। এই পদ্ধতি ব্যবহার করলে যে পর্যবেক্ষকরা পরস্পর সাপেক্ষ চলমান তাঁরা একই ঘটনাকে ভিন্ন ভিন্ন স্থানে এবং কালে আরোপ করবেন। কোনো বিশেষ পর্যবেক্ষকের মাপন অন্য কোনো পর্যবেক্ষকের মাপনের চাইতে বেশি নির্ভুল নয়। তবে প্রতিটি মাপনের ভিতরেই একটা সম্পর্ক রয়েছে। যে কোনো পর্যবেক্ষকই একটি ঘটনা সাপেক্ষ অন্য একজন পর্যবেক্ষক কি কাল এবং অবস্থান আরোপ করবেন সেটা হিসাব করে বলতে পারবেন- অবশ্য তিনি যদি আর একজনের আপেক্ষিক গতিবেগ জানেন।
আজকাল আমরা দূরত্ব নির্ভুলভাবে নির্ণয় করার জন্য এই পদ্ধতিই ব্যবহার করি। কারণ, আমরা দৈর্ঘ্যের চাইতে কাল অনেক নির্ভুলভাবে মাপতে পারি। কার্যক্ষেত্রে মিটারের সংজ্ঞা আলোক ০.০০০০০০০০৩৩৩৫৬৪০৯৫২ সেকেন্ডে যে দূরত্ব অতিক্রম করে, সেই দূরত্ব। কাল মাপা হয় একটি সিসয়াম (cesium) ঘড়ি দিয়ে। (এই বিশেষ সংখ্যার কারণ হলঃ এটা মিটারের ঐতিহাসিক সংজ্ঞার অনুরূপ- প্যারিসে রক্ষিত একটি বিশেষ প্ল্যাটিনাম দন্ডে অঙ্কিত দুটি চিহ্নের বাগ্বিধিতে)। একই ভাবে আমরা আলোক সেকেন্ড নামক আরো সুবিধাজনক নতুন একটি দৈর্ঘ্যের একক ব্যবহার করতে পারি। এটার সংজ্ঞা শুধুমাত্র এক সেকেন্ডে আলোক যে দূরত্ব অতিক্রম করে সেই দৈর্ঘ্য। অপেক্ষবাদ আজকাল আমরা দূরত্বের সংজ্ঞা নির্ধারণ করি কাল এবং আলোকের দ্রুতির বাগ্বিধিতে (in terms of)। সুতরাং এর স্বাভাবিক ফলশ্রুতি হল প্রতিটি পর্যবেক্ষকের মাপনে আলোকের গতিবেগ একই হবে (সংজ্ঞা অনুসারে প্রতি ০.০০০০০০০০৩৩৩৫৬৪০৯৫২ সেকেন্ডে এক মিটার)। ইথার সম্পর্কীয় ধারণা উপস্থিত করার কোনো প্রয়োজন নেই। মিচেলসন-মর্লি পরীক্ষায় দেখা গিয়েছে ইথারের অস্তিত্ব কোনোক্রমেই আবিষ্কার করা যায় নি। অপেক্ষবাদ কিন্তু স্থান এবং কাল সম্পর্কে আমাদের ধারণা মূলগতভাবে পরিবর্তিত করতে বাধ্য করে। আমাদের মানতেই হবেঃ কাল স্থান
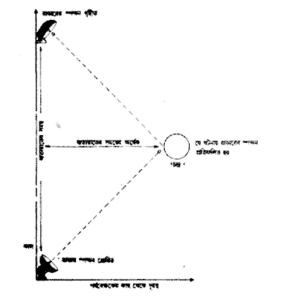
থেকে সম্পূর্ণ বিচ্ছিন্ন নয় এবং স্থান নিরপেক্ষও নয়। বরং এ দুটির সমন্বয়ে স্থান-কাল নামক বস্তু গঠিত হয়েছে।
সাধারণ অভিজ্ঞতায় বলে স্থানে একটি বিন্দুর অবস্থান তিনটি সংখ্যা কিম্বা তিনটি স্থানাঙ্ক দিয়ে নির্দিষ্ট করা যায়। উদাহরণ, বলা যায় ঘরের একটি বিন্দু একটি দেওয়াল থেকে সাত ফুট দূরে, আর একটি দেওয়াল থেকে তিন ফুট দূরে এবং মেঝে থেকে পাঁচ ফুট উপরে। কিম্বা নির্দেশ করা যায় একটি বিন্দু একটি বিশেষ অক্ষাংশ (latitude) এবং একটি বিশেষ দ্রাঘিমায় (longitude) এবং সমুদ্রতলের উপরে একটি বিশেষ উচতায় অবস্থিত ছিল। স্বাধীনভাবে যে কোনো তিনটি স্থানাঙ্ক বেছে নেওয়া যেতে পারে, অবশ্য সেগুলির সত্যতার ব্যাপ্তি সীমিত। চাঁদের অবস্থান নির্দেশ করতে হলে কেউ পিকাডিলি সার্কাস থেকে কত মাইল উত্তরে এবং কত মাইল পশ্চিমে এবং সমুদ্রতল থেকে কত ফুট উচ্চতায়-এই বাগ্বিধি ব্যবহার করে না। তার বদলে সূর্য থেকে দূরত্ব কিম্বা কোনো গ্রহের কক্ষতল (plane of orbit) থেকে দূরত্বের বাগ্বিধিতে এবং সূর্য ও চন্দ্রকে সংযোগকারী রেখা এবং সূর্য ও আলফা সেন্টেরীর (Alpha Centuri) মতো কোনো একটি নক্ষত্রকে সংযোগকারী রেখা দ্বারা গঠিত কোণের বাগ্বিধিতে নির্দেশ করা যায়। আমাদের ছায়াপথে সূর্যের অবস্থানের বিবরণ দিতে হলে এই স্থানাঙ্কগুলি দিয়ে খুব সুবিধা হয় না। আমাদের ছায়াপথ (galaxy) গোষ্ঠীর ভিতরে আমাদের ছায়াপথের অবস্থান নির্দেশ করতে হলে এই স্থানাঙ্কগুলি দিয়েও খুব সুবিধা হয় না। আসলে সমগ্র মহাবিশ্বের বিবরণ কয়েকটি পরস্পর আবৃতকারী (overlapping) অংশের (patches) সমষ্টি রূপে দেওয়া যেতে পারে। প্রতিটি অংশের একটি বিন্দুর অবস্থান নির্দিষ্ট করার জন্য বিভিন্ন কেতাব (set) তিনটি স্থানাঙ্ক ব্যবহার করা যায়।
একটি ঘটনা হল এমন একটি জিনিষ যা স্থানের একটি বিন্দুতে এবং একটি বিশেষ কালে ঘটে। সুতরাং, চারটি সংখ্যা বা স্থানাঙ্ক দিয়ে তাকে নির্দিষ্ট করা সম্ভব। এ ক্ষেত্রেও স্থানাঙ্ক নির্বাচন যাদৃচ্ছিক (arbitrary)। যে কোনো তিনটি স্থানিক স্থানাঙ্ক এবং কালের যে কোনো মাপন ব্যবহার করা যেতে পারে। অপেক্ষবাদে স্থানিক এবং কালিক স্থানাঙ্কের ভিতরে বাস্তবে কোনো পার্থক্য নেই। ঠিক যেমন নেই, দুটি স্থানিক স্থানাঙ্কের ভিতরে। স্থানাঙ্কের একটি নতুন কেতা (set) বেছে নেওয়া যেতে পারে। ধরুন- সেটাতে আগেকার প্রথম এবং দ্বিতীয়ের সমন্বয় করে প্রথম স্থানাঙ্কটি হয়েছিল। উদাহরণঃ পৃথিবীর উপরে একটি বিন্দুর অবস্থান পিকাডিলি থেকে উত্তরে কয়েক মাইল এবং পশ্চিমে কয়েক মাইল হিসাবে না মেপে, পিকাডিলি থেকে উত্তর-পূর্বে কয়েক মাইল এবং উত্তর-পশ্চিমে কয়েক মাইল হিসাবে না মেপে, পিকাডিলি থেকে উত্তর-পূর্বে কয়েক মাইল এবং উত্তর-পশ্চিমে কয়েক মাইল করেও মাপা যেতে পারে। তেমনি, অপেক্ষবাদে প্রাচীন কাল (সেকেন্ডে) এবং পিকাডিলি থেকে দূরত্বের (আলোক সেকেন্ডে) সমন্বয় করে একটি নতুন কালিক স্থানাঙ্ক ব্যবহার করা যেতে পারে।
অনেক সময় একটি ঘটনার অবস্থান চার মাত্রিক স্থানে (four dimensional space) অর্থাৎ স্থান-কাল নির্দিষ্ট করার জন্য চারটি স্থানাঙ্কের বাগ্বিধিতে চিন্তা করা সুবিধা। এর নাম স্থান-কাল। চারমাত্রিক স্থান কল্পনা করা অসম্ভব। ব্যক্তিগতভাবে আমার পক্ষে ত্রিমাত্রিক স্থানের দৃষ্টিকল্পন (visualize) করাই বেশি কঠিন। কিন্তু দ্বিমাত্রিক স্থানের, যথা পৃথিবীর পৃষ্ঠের (surface) মতো স্থানের চিত্রাঙ্কন সহজ [পৃথিবীর পৃষ্ঠ দ্বিমাত্রিক, কারণ, দু’টি স্থানাঙ্ক দিয়ে একটি বিন্দুর অবস্থান নির্দিষ্ট করা যায়ঃ দ্রাঘিমা এবং অক্ষাংশ (longitude & latitude)] আস্মি সাধারণত এমন চিত্র ব্যবহার করব- যাতে কাল বৃদ্ধি পায় উপর দিকে এবং স্থানিক মাত্রাগুলির একটি দেখানো হয় আনুভূমিকভাবে (horizontally)। অন্য দুটি স্থানিক মাত্রা অগ্রাহ্য করা হয় কিম্বা অনেক সময় তাঁদের একটি দেখানো হয় দর্শনানুপাতের (perspective) সাহায্যে। (এগুলিকে বলা হয় স্থান-কাল চিত্র, চিত্র ২.১- এর মতো।) উদাহরণঃ চিত্রা ২.২- এ কাল মাপা হয়েছে বৎসর হিসাবে এবং ঊর্ধ্বদিকে। আলফা সেন্টোরী (Alpha Centauri) থেকে সূর্য বরাবর দূরত্ব মাপা হয়েছে মাইল হিসাবে আনুভূমিকভাবে। স্থান-কালের ভিতর দিয়ে সূর্য এবং আলফা সেন্টোরীর (Alpha Centauri) পথ দেখানো হয়েছে চিত্রের ডান ও বাম পাশে উল্লম্ব রেখা দিয়ে। সূর্য থেকে আগত একটি আলোকরশ্মি কর্ণরেখা (diagonal line) অনুসরণ করে এবং সূর্য থকে আলফা সেন্টোরী যেতে চার বছর সময় নেয়।
আমরা দেখছি ম্যাক্সওয়েলের সমীকরণ ভবিষ্যদ্বাণী করেছিল আলোকের উৎসের দ্রুতি যাই হোক না কেন, আলোকের দ্রুতি একই থাকবে। এই তথ্যের সত্যতা নিখুঁত মাপনের সাহায্যে প্রমাণিত হয়েছে। এর ফলশ্রুতি হল যদি একটি বিশেষ কালে স্থানের একটি বিশেষ
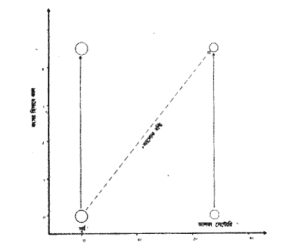
বিন্দুতে আলোকের একটি স্পন্দন উৎসারিত হয়, তাহলে কালের গতির সঙ্গে সঙ্গে সেটা একটা আলোকের গোলকরূপে বিস্তার লাভ করবে। তার আকার এবং অবস্থান হবে উৎসের গতিনিরপেক্ষ। এক সেকেন্ডের এক মিলিয়ন (১০,০০,০০০) ভাগের এক ভাগ সময়ে
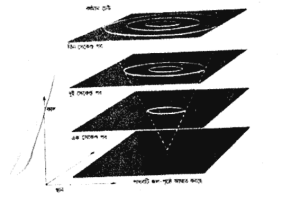
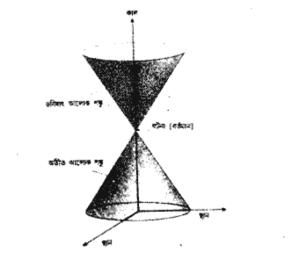
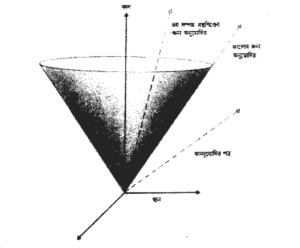
আলোক বিস্তার লাভ করে এমন একটা গোলক গঠন করবে যার ব্যাসার্ধ হবে ৩০০ মিটার। এক সেকেন্ডের এক মিলিয়ন ভাগের দুভাগে ব্যাসার্ধ হবে ৬০০ মিটার এবং এইভাবে চলবে। ব্যাপারটা একটা পুকুরের পৃষ্ঠে (surface) ঢিল ফেললে ঢেউগুলি যেভাবে বিস্তার লাভ করে অনেকটা সেই রকম। ঢেউগুলি বিস্তার লাভ করে একটি বৃত্তরূপে এবং বলের গতির সঙ্গে সঙ্গে বৃত্তটি আকারে বাড়ে। যদি পুকুরের পৃষ্ঠের দুই মাত্রা এবং কালের এক মাত্রা মিলিয়ে একটি ত্রিমাতৃক প্রতিরূপের কথা ভাবা যায় তাহলে ঢেউয়ের বিস্তারমান বৃত্তে একটি শঙ্কু (conc) সৃষ্টি করবে। শঙ্কুর প্রারম্ভিক শীর্ষবিন্দু থাকবে সেই স্থান-কালে যেখানে ঢিলটি জলে আঘাত করেছিল (চিত্র- ২.৩)। একইভাবে একটি ঘটনা থেকে বিস্তারমান আলোর চারমাত্রিক স্থান-কালে একটি ত্রিমাতৃক শঙ্কু সৃষ্টি করে। এই শঙ্কুকে বলা হয় ঘটনার ভবিষ্যৎ আলোক শঙ্কু।

এইভাবেই আমরা অতীত আলোক শঙ্কু নামে আর একটি শঙ্কু আঁকতে পারি। সেগুলি এমন কতগুলি ঘটনার কেতা (set) যেখান থেকে আলোকের একটি স্পন্দন নির্দিষ্ট ঘটনায় পৌঁছাতে পারে। (চিত্র- ২.৪)।
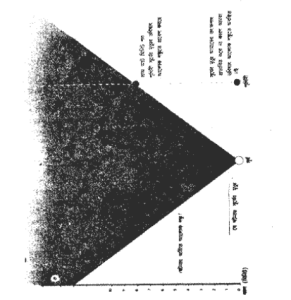
একটি ঘটনা P- এর ভবিষ্যৎ এবং অতীত আলোক শঙ্কু স্থান-কালকে তিনভাগে বিভক্ত করে (২.৫ চিত্র)। ঘটনাটির পরম ভবিষ্যৎ হল আলোক শঙ্কু (conc) P-এর ভিতরকার একটি অঞ্চল। এটি হল P- তে যা ঘটনা ঘটে সেটা সম্ভাব্য যত ভাবে প্রভাবিত হতে পারে সে রকম সব ঘটনার একটি কেতা (set of all events)। আলোক শঙ্কু P-এর বাইরের ঘটনায় কখনো P- থেকে উৎসারিত সংকেত পৌঁছাতে পারে না। তার কারণ, কোন কিছুইন আলোকেই চেয়ে দ্রুততর যেতে পারে না। সুতরাং P- তে কি ঘটছে তাই দিয়ে তারা প্রভাবিত হতে পারে না। অতীত আলোক শঙ্কুর অন্তর্বর্তী অঞ্চলই P এর পরম অতীত (absolute past)। আলোকের দ্রুতি কিম্বা তার নিম্নতর দ্রুতিতে চলমান যে সমস্ত সংকেত সমস্ত ঘটনার কেতা (set of all events) থেকে P-তে পৌঁছাতে পারে, এ হল তাই। সুতরাং এটা হল সেই সমস্ত ঘটনার কেতা যার P-তে যা ঘটছে তাকে প্রভাবিত করার সম্ভাবনা আছে। কোন বিশেষকালে স্থানের যে অঞ্চল P- এর অতীত আলোক শঙ্কুর অন্তর্ভুক্ত, সে অঞ্চলের প্রত্যেক স্থানে যা ঘটছে তা যদি জানা থাকে তাহলে P-তে কি ঘটবে সে সম্বন্ধে ভবিষ্যদ্বাণী করা সম্ভব। অন্য স্থান হল স্থান-কালের সেই অঞ্চল যা P-এর অতীত কিম্বা ভবিষ্যৎ আলোক শঙ্কুর অন্তর্ভুক্ত নয়। সেই অন্য স্থানের ঘটনা P-তে সংঘটিত ঘটনাগুলিকে প্রভাবিত করতে পারে না কিম্বা তাদের দ্বারা প্রভাবিত হতেও পারে না। উদাহরণঃ যদি এই মুহূর্তেই সূর্য আলোক বিকিরণ বন্ধ করে দেয় তাহলে বর্তমান কালে পৃথিবীতে অবস্থিত জিনিসের উপর তার কোন প্রভাব পড়বে না। তার কারণ, সূর্য যখন নিভে গেল (চিত্র- ২.৬) তখন পৃথিবীর জিনিসগুলি থাকবে ঘটনার অন্য অঞ্চলে। ব্যাপারটা আমরা জানতে পারব শুধু আট মিনিট পর। অর্থাৎ সূর্য থেকে আমাদের কাছে আলো পৌঁছাতে যে সময় লাগে তারপর। শুধুমাত্র সেই সময়ই পৃথিবীস্থ ঘটনাবলি সূর্যের নিভে যাওয়ার ঘটনার ভবিষ্যৎ আলোক শঙ্কুর অন্তর্ভুক্ত হবে। একইভাবে বলা যায় এই মুহূর্তে এই মহাবিশ্বের দূরতর অঞ্চলে কি ঘটছে তা আমরা জানি না। সুদূরের নীহারিকা থেকে আগত যে আলোক আমরা দেখি সে আলোক বহু মিলিয়ন বৎসর আগে সেই নীহারিকাগুলি থেকে রওয়ানা হয়েছিল। দূরতম যে বস্তু আমরা দেখতে পাই, তাদের ক্ষেত্রে আলোক রওয়ানা হয়েছে প্রায় আট হাজার মিলিয়ন বছর আগে। সুতরাং যখন আমরা মহাবিশ্ব দেখি তখন আসলে দেখতে পাই মহাবিশ্বের অতীত রূপ।
আইনস্টাইন এবং পয়েনকেয়ার ১৯০৫ সালে যা করেছিলেন, মহাকর্ষীয় অভিক্রিয়াকে যদি সেই রকম অগ্রাহ্য করা যায় তাহলে যা হবে সেটা হল বিশিষ্ট অপেক্ষবাদ। স্থান-কালের প্রতিটি ঘটনবা সাপেক্ষেই আমরা একটি আলোক শঙ্কু গঠন করতে পারি [সেই ঘটনার (at the event) স্থান-কালে উৎসারিত আলোকের সম্ভাব্য সমস্ত গতিপথের কেতা (set)] এবং যেহেতু প্রতিটা ঘটনা সাপেক্ষ এবং প্রতিটি অভিমুখেই আলোর দ্রুতি এক, সেই জন্য সমস্ত আলোক শঙ্কুই হবে সমরূপ এবং সবগুলির অভিমুখই হবে এক। এই তত্ত্ব আরো বলে আলোকের চাইতে দ্রুতগতি কারো হতে পারে না। এই অর্থ বল স্থান-কালের ভিতর দিয়ে যে কোন বস্তুরই গতিপথের প্রতিরূপ এমন একটি রেখা যা তার উপরে প্রতিটি ঘটনার আলোক শঙ্কুর অভ্যন্তরে অবস্থিত।
সমস্ত পর্যবেক্ষক সাপেক্ষই আলোকের দ্রুতই অভিন্ন (মিচেলসন-মর্লির পরীক্ষাতে এটাই দেখানো হয়েছে)। এই তত্ত্ব ব্যাখ্যায় এবং যখন কোনো বস্তু আলোকের দ্রুতির কাছাকাছি দ্রুতিতে চলমান হয় তখন কি ঘটে তার বিব্রণ্ম দেওয়ার ব্যাপারে বিশিষ্ট অপেক্ষবাদ খুবই সাফল্য লাভ করে। নিউটনের মহাকর্ষীয় তত্ত্বের সঙ্গে এর কিন্তু অসঙ্গতি ছিল। সে তত্ত্বের মতে বস্তুগুলি পরস্পরকে আকর্ষণ করে এবং আকর্ষণ বল তাদের অন্তর্বর্তী দূরত্বের উপর নির্ভরশীল। এর অর্থ হলঃ একটি বস্তুকে যদি সরানো যায় তাহলে অন্য বস্তুটির উপরে প্রযুক্ত বলের তাৎক্ষণিক পরিবর্তন হবে। কিম্বা অন্য ভাবে বলা যায়, মহাকর্ষীয় অভিক্রিয়ার অসীম গতিতে চলমান হওয়া উচিত। অথচ বিশিষ্ট অপেক্ষবাদের দাবী মহাকর্ষীয় বলের দ্রুতি হওয়া উচিত আলোর দ্রুতির সমান বা তার চাইতে কম। ১৯০৮ সাল থেকে ১৯১৪ সাল পর্যন্ত আইনস্টাইন চেষ্টা করেছেন এমন একটি মহাকর্ষীয় তত্ত্ব আবিষ্কার করতে যার সঙ্গে বিশিষ্ট অপেক্ষবাদের সঙ্গতি থাকবে। কিন্তু তিনি সফল হন নি। শেষে ১৯১৫ সালে আমরা যাকে ব্যাপক অপেক্ষবাদ বলি সেই তত্ত্ব তিনি উপস্থিত করেন।

আইনস্টাইন এই বিপ্লবী প্রস্তাব উত্থাপন করেন যে, মহাকর্ষীয় বল অন্যান্য বলের মতো নয়। আগে যেরকম অনুমান করা গিয়েছিল স্থান-কাল সেরকম সমতল (flat) নয়, এটা বক্র কিম্বা বঙ্কিম (warped)। তার কারণ, স্থান-কালে ভর এবং শক্তির বন্টন। আইনস্টাইনের মতে মহাকর্ষ এরই ফলশ্রুতি। পৃথিবীর মতো বস্তুপিন্ড যে বঙ্কিম কক্ষে চলে তার কারণ মহাকর্ষ নামক বল নয়, তারা বঙ্কিম স্থানে ঋজুপথের নিকটতম পথ অনুসরণ করে। সে পথের নাম জিওডেসিক। উদাহরণঃ পৃথিবীর পৃষ্ঠদেশ (surface) একটি দ্বিমাত্রিক বঙ্কিম স্থান। পৃথিবীর উপরের জিওডেসিককে বলা হয় বৃহৎ বৃত্ত (great circle) এবং দুটি বিন্দুর ভিতরে এতাই হ্রস্বতম পথ সেইজন্য বিমানের নাবিক (navigator) বিমানচালককে এই পথে যেতে বলে। ব্যাপক অপেক্ষবাদে বস্তুপিন্ডগুলি সব সময়ই চতুর্মাত্রিক স্থান-কালে ঋজুরেখা অনুসরণ করে। কিন্তু আমাদের মনে হয় তারা আমাদের ত্রিমাত্রিক স্থানে বঙ্কিম পথে চলমান। (এটা অনেকটা পর্বতময় জমির উপর দিয়ে চলমান বিমান দেখার মতো। বিমানটি ত্রিমাত্রিক স্থানে একটি সরলরেখা অনুসরণ করে, কিন্তু এর ছায়া দ্বিমাত্রিক ভূমির উপর একটি বঙ্কিম পথ অনুসরণ করে)।

সূর্যের ভর স্থান-কালকে এমনভাবে বাঁকিয়ে দেয় যে পৃথিবীর যদিও চতুর্মাত্রিক স্থান-কালে ঋজুপথ অনুসরণ করে, তবুও আমাদের মনে হয় পৃথিবী ত্রিমাত্রিক স্থানে বৃত্তাকায় কক্ষে চলমান। আসলে ব্যাপক অপেক্ষবাদ গ্রহগুলির কক্ষ সম্পর্কে যে ভবিষ্যদ্বাণী করছে তা মহাকর্ষ বিষয়ে নিউটনীয় তত্ত্বের সঙ্গে প্রায়া নির্ভুলভাবে অভিন্ন। বুধগ্রহ সূর্যের নিকটতম এবং মহাকর্ষীয় অভিক্রিয়া তার ক্ষেত্রে সবচাইতে শক্তিশালী। তাছাড়া তার কক্ষ একটু লম্বাটে। ব্যাপক অপেক্ষবাদ কিন্তু ভবিষ্যদ্বাণী করেছে এই উপবৃত্তের দীর্ঘ অক্ষ (long axis) সূর্যের চতুষ্পার্শ্বে বৃত্তাকারে ১০,০০০ বছরে এক ডিগ্রী হিসাবে ঘুরবে। এই অভিক্রিয়া ক্ষুদ্র হলেও ১৯১৫ সালের আগেই এটা দেখা গিয়েছিল এবং আইনস্টাইনের তত্ত্বের সত্যতা প্রমাণের প্রথম সাক্ষ্যগুলির ভিতরে এটি ছিল একটি। আধুনিক কয়েক বছরে অন্যান্য গ্রহগুলির কক্ষের (orbit) নিউটনীয় ভবিষ্যদ্বাণী থেকে আরও ক্ষুদ্রতর বিচ্যুতি, রাডার (Radar)- এর সাহায্যে মাপা হয়েছে। দেখা গিয়েছে, ব্যাপক অপেক্ষবাদের ভবিষ্যদ্বাণীর সঙ্গে তার ঐক্য রয়েছে।
আলোক রশ্মিকে স্থান-কালে জিওডেসিক অবশ্যই অনুসরণ করতে হবে। তাছাড়া স্থান যে বক্র এই তথ্যের অর্থ হলঃ স্থানে আলোককে আর ঋজুরেখায় চলমান বলে মনে হবে না। সুতরাং ব্যাপক অপেক্ষবাদের ভবিষ্যদ্বাণী হল, মহাকর্ষীয় ক্ষেত্র আলোককে বাঁকিয়ে দেবে। উদাহরণঃ এই তত্ত্বের ভবিষ্যদ্বাণী অনুসারে সূর্যের নিকটবর্তী বিন্দুগুলির আলোক শঙ্কু সূর্যের ভরের জন্য অন্তর অভিমুখে সামান্য বঙ্কিম হবে। এর অর্থ হল, দূরবর্তী তারকা থেকে নির্গত আলোক সূর্যের কাছ দিয়ে যাওয়ার সময় বিচ্যুত (deflected) হবে। এই বিচ্যুতির কোণ হবে সামান্য। ফলে পৃথিবীর পৃথিবীর একজন পর্যবেক্ষক সাপেক্ষ তারকাটিতে ভিন্ন স্থানে অবস্থিত বলে মনে হবে (চিত্র- ২.৯)। অবশ্য তারকাটি থেকে আলোক যদি সব সময়ই সূর্যের নিকট দিয়ে গমন করে তাহলে আলোক বিচ্যুত (deflected) হচ্ছে, না কি তারকাটি যেখানে দেখা যাচ্ছে সেখানেই অবস্থিত- সেটা আমরা বলতে পারব না। কিন্তু পৃথিবী যখন সূর্যকে প্রদক্ষিণ করে তখন বিভিন্ন তারকাকে সূর্যের পশ্চাদবর্তী বলে মনে হয় এবং তাদের আলোকের বিচ্যুতি ঘটে। সুতরাং সূর্য সাপেক্ষ তাদের আপাতদৃষ্ট অবস্থানের পরিবর্তন হয়।
এই অভিক্রিয়া স্বাভাবিক অবস্থায় দেখা খুব শক্ত। তার কারণ, সূর্যের আলোকের দরুন যে সমস্ত তারকা সূর্যের নিকটবর্তী সেগুলিকে পর্যবেক্ষণ করা অসম্ভব হয়ে দাঁড়ায়। কিন্তু সূর্যগ্রহণের সময় এই পর্যবেক্ষণ সম্ভব। তখন সূর্যের আলোককে চাঁদ আটকে দেয়। ১৯১৫ সালে আলোকের বিচ্যুতি সম্পর্কে আইনস্টাইনের ভবিষ্যদ্বাণীর তাৎক্ষণিক পরীক্ষা সম্ভব হয়নি। কারণ, তখন প্রথম বিশ্বযুদ্ধ চলছিল। ১৯১৯ সালের আগে পর্যন্ত এ পরীক্ষা হয়নি। ১৯১৯ সালে একটি ব্রিটিশ অভিযাত্রী দল পশ্চিম আফ্রিকা থেকে একটি গ্রহণ পরীক্ষা করে দেখিয়েছিলেন, আলোক সত্যিই সূর্য দ্বারা বিচ্যুত (deflected) হয়। অর্থাৎ তত্ত্ব যা ভবিষ্যদ্বাণী করেছে, তাই হয়। একটি জার্মান তত্ত্ব ব্রিটিশ বৈজ্ঞানিক দ্বারা প্রমাণিত হওয়া তখনকার দিনে অর্থাৎ প্রথম বিশ্বযুদ্ধের পর দুটি দেশের পুনঃস্থাপনের সপক্ষে একটি পদক্ষেপ বলে অভিনন্দিত হয়েছিল। সেইজন্য ব্যাপারটি যেন একটা পরিহাস। তার কারণ, সেই অভিযানে যে আলোকচিত্রগুলি নেওয়া হয়েছিল পরে সেগুলি পরীক্ষা করে দেখা গিয়েছে, তাঁরা যে অভিক্রিয়া মাপতে চেষ্টা করেছিলেন আলোকচিত্রগুলিতে ভুল ছিল তার সমান সমান। তাঁদের মাপনটা ছিল নেহাৎই সৌভাগ্যের ব্যাপার। কিম্বা তাঁরা যে ফল পেতে চেয়েছিলেন সেটা আগে থাকতেই জানা থাকার দরুনই ব্যাপারটা ঘটেছিল। বিজ্ঞানে এরকম ঘটনা ঘটা অস্বাভাবিক নয়। তবে পরবর্তী কয়েকটি পর্যবেক্ষণে আলোকের এই বিচ্যুতি যে সত্য সেটা নির্ভুলভাবে দেখা গিয়েছে।
ব্যাপক অপেক্ষবাদের আর একটি ভবিষ্যদ্বাণী হল, পৃথিবীর মতো গুরু ভর সম্পন্ন কোনো বস্তুপিন্ডের সন্নিকটে সময়ের গতি শ্লথ বলে মনে হবে। তার কারণ, আলোকের স্পন্দাঙ্ক (frequency)- অর্থাৎ সেকেন্ড প্রতি আলোক তরঙ্গের সংখ্যা) এবং আলোকের শক্তির ভিতরে একটি সম্পর্ক রয়েছে। শক্তি যত বেশি হবে স্থানাঙ্ক তত বাড়বে। আলোক পৃথিবীর মহাকর্ষীয় ক্ষেত্রের ভিতর দিয়ে যত উপরে যাবে ততই তার শক্তি ক্ষয় হবে। সুতরাং তার কম্পাঙ্ক কমে যাবে (এর অর্থ হল একটি তরঙ্গশীর্ষ থেকে পরবর্তী তরঙ্গশীর্ষের মধ্যবর্তী কালের দৈর্ঘ্য বৃদ্ধিপ্রাপ্ত হবে)। খুব উচ্চে অবস্থিত কোনো লোকের মনে হবে নিচের সব ঘটনাই একটু দেরিতে ঘটছে। এই ভবিষ্যদ্বাণী পরীক্ষা করা হয়েছিল ১৯৬২ সালে। তখন একটি জলধারার স্তম্ভের উপরে এবং নিচে একজোড়া নির্ভুল ঘড়ি স্থাপন করা হয়েছিল। যে ঘড়িটা নিচে ছিল অর্থাৎ পৃথিবীর নিকটতর ছিল, দেখা গেল তার প্রতি ধীরতর। এ তথ্যের সঙ্গেও ব্যাপক অপেক্ষবাদের নির্ভুল ঐক্য রয়েছে। আধুনিক কালে পৃথিবীর উপরে বিভিন্ন উচ্চতায় স্থাপিত বিভিন্ন ঘড়ির দ্রুতির পার্থক্যের যথেষ্ট ব্যবহারিক গুরুত্ব রয়েছে। কৃত্রিম উপগ্রহ (satellites) থেকে আগত সঙ্কেতের ভিত্তিতে নির্ভুল নৌ এবং বিমান চালন ব্যবস্থার অভ্যুদয়ের সঙ্গে সঙ্গেই এর গুরুত্ব বেড়েছে। ব্যাপক অপেক্ষবাদের ভবিষ্যদ্বাণী অগ্রাহ্য করলে অবস্থানের হিসাবে কয়েক মাইল পর্যন্ত ভুল হতে পারে।
নিউটনের গতি বিষয়ক বিধি স্থানে পরম অবস্থান সম্পর্কীয় চিন্তাধারা একদম শেষ করে দেয়। অপেক্ষবাদ শেষ করেছে পরম কালকে। এক জোড়া যমজের কথা ভাবা যাক। অনুমান করা হোক্ম একজন থাকল একটি পাহাড়ের চুড়াতে আর একজন বইল সমুদ্রপৃষ্ঠের উচ্চতায় অবস্থিত কোনো সমতলে। প্রথম জনের বয়স দ্বিতীয় জনের তুলনায় তাড়াতাড়ি বাড়বে। সুতরাং তাদের যদি আবার দেখা হয় তাহলে একজনকে আর একজনের চাইতে বয়স্ক বলে মনে হবে। এক্ষেত্রে বয়সের পার্থক্যটা হবে অতি সামান্য। কিন্তু পার্থক্যটা বেশি হবে যদি তাঁদের ভিতরে একজন মহাকাশ যানে চড়ে আলোকের দ্রুতির কাছাকাছি দ্রুতিতে ভ্রমণ করতে বার হয়। যখন সে ফিরবে তখন সে পৃথিবীতে যে ছিল তার তুলনায় অনেক বেশি তরুণ থাকবে। এ ব্যাপারটাকে বলা হয় যমজ সম্পর্কীয় স্ববিরোধ (twin paradox)। কিন্তু এটা শুধুমাত্র তখনই স্ববিরোধ, যখন মনের ভিতরে পরম কাল সম্পর্কে ধারণা রয়েছে। অপেক্ষবাদে কোনো অনন্য পরম কালের অস্তিত্ব নেই, তার বদলে রয়েছে প্রতিটি ব্যক্তির কালের নিজস্ব মাপন। সেটা নির্ভর করে তার অবস্থানের উপরে এবং সে কি ভাবে চলমান তার উপরে।
১৯১৫ সালের আগে ধারণা ছিল স্থান এবং কাল এক একটি স্থির ক্ষেত্র (atena)। ঘটনাগুলি ঘটে সেখানে, কিন্তু সেখানে যা ঘটেছে তার দ্বারা ক্ষেত্রটি নিজে প্রভাবিত হয় না। এমন কি বিশিষ্ট অপেক্ষবাদের ক্ষেত্রেও এটাই ছিল সত্য। বস্তুপিন্ডগুলি চলমান। তারা পরস্পরকে আকর্ষণ কিম্বা বিকর্ষণ করে কিন্তু এবং স্থান নিরবধি, তার কোনো বিকার নেই (continued unaffected)। স্থান এবং কালকে চিরস্থায়ী ভাবাই ছিল স্বাভাবিক।
কিন্তু ব্যাপক অপেক্ষবাদে পরিস্থিতিটা অনেকটাই অন্যরকম। এখন স্থান এবং কাল গতিশীল রাশি। একটি বস্তুপিন্ড যখন চলমান কিম্বা একটি বল যখন ক্রিয়াশীল, তখন সে স্থান-কালের বক্রতা প্রভাবিত করে এবং স্থান ও কালের গঠন আবার প্রভাবিত করে বস্তুপিন্ডগুলির চলন এবং বিভিন্ন বলের ক্রিয়া। মহাবিশ্বে যা কিছু ঘটছে সেগুলি শুধু স্থান-কালকে প্রভাবিত করে তাই নয়, স্থান-কাল নিজেরাও তাদের দ্বারা প্রভাবিত হয়। ঠিক যেমন মহাবিশ্বে যে ঘটনাগুলি ঘটছে স্থান-কাল সম্পর্কে ধারণা ছাড়া সেগুলি সম্পর্কে বলা সম্ভব নয়। ব্যাপক অপেক্ষবাদেও তেমনি মহাবিশ্বের সীমানার বাইরে স্থান-কাল সম্পর্কে বলা অর্থহীন।
পরবর্তী দশকগুলিতে স্থান-কাল সম্পর্কে এই নতুন বোধ (understanding) আমাদের মহাবিশ্ব সম্পর্কীয় ধারণায় বিপ্লব এনেছে। আমাদের প্রাচীন ধারণা ছিলঃ মহাবিশ্ব মূলত অপরিবর্তনীয়। তার অস্তিত্ব চিরকাল ছিল এবং থাকবে। এর জায়গায় বর্তমান ধারণাঃ মহাবিশ্ব গতিশীল এবং প্রসারমান। সীমিতকাল পূর্বে তার শত্রু এবং ভবিষ্যতে সীমিতকাল পরে তার শেষও হতে পারে। পরবর্তী অধ্যায়ের বিষয়বস্তু এই বিপ্লব। বহু বছর পরে তাত্ত্বিক পদার্থবিদ্যায় আমার গবেষণা শুরু হয়েছিল এই বিন্দু থেকে। রজার পেনরোজ (Roger Penrose) এবং আমি দেখিয়েছিলাম, আইনস্টাইনের ব্যাপক অপেক্ষবাদের ভিতরে নিহিত রয়েছে এই তত্ত্ব অর্থাৎ মহাবিশ্বের একটি শুরু রয়েছে এবং হয়তো একটা শেষও আছে।
“কালের সংক্ষিপ্ত ইতিহাস” বই সম্পর্কিত আপনার মন্তব্যঃ