পঞ্চম অধ্যায়ঃ প্রকৃতির শূন্যবিদ্বেষ ?

‘উন্মুক্ত আকাশ বসে আছে দেয়ালে হেলান দিয়ে।

যেন প্রার্থনায় মগ্ন এক মহাশূন্যতায়।

আর এই মহাশূন্যতায় কে যেন

আমাদের চোখে চোখ রেখে বলে যায়,

আমি শূন্য নই,আমি উন্মুক্ত’।

—টমাস ট্রান্সট্রোমার,আমি শূন্য নই,আমি উন্মুক্ত

ঠিক আছে, ‘শূন্যের’ একটা ঠিকানা হয়ে গেল অবশেষে; বাস্তবে না হলেও গণিতের পৃষ্ঠায়, চিন্তায়, দর্শনেও হয়তো বা। কিন্তু প্রশ্ন থেকে যায় তখনো। সত্যি সত্যি কি শূন্য বলে কিছু আছে প্রকৃতিতে? অ্যারিস্টটলের তত্ত্ব অনুযায়ী: শূন্য অস্তিত্বহীন। শূন্যাবস্থাকে ঘোর অপছন্দ করে প্রকৃতি (nature abhors a vacuum)। তার অর্থ জড়জগতে ফাঁকা জায়গা নেই কোনোখানে। ফাঁকা উপক্রম হওয়ামাত্র প্রকৃতি তাকে ভরাট করার জন্য উঠেপড়ে লেগে যাবে। সত্যি কি তাই? এটা কি কেবলই বিশ্বাস, না, বৈজ্ঞানিক তথ্য? গ্যালিলিওর জীবনকালে ইতালির একদল শ্রমিক একটা সমস্যা নিয়ে এসেছিলেন তাঁর কাছে। কুয়ো থেকে নল আর পিস্টনের সাহায্যে, বা খাল থেকে পানি তোলার সময় দেখা যায় যে নলের ওপর দিকটায় খালি জায়গা থাকা সত্ত্বেও পানি বড়জোর ৩৩ ফুট পর্যন্ত ওঠে, তার ওপরে কিছুতেই তোলা যায় না, হাজার পরিশ্রম করেও না। তার কারণটা কী?

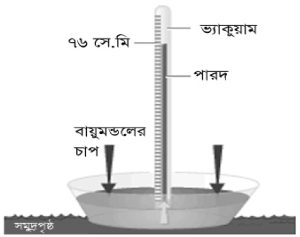
গ্যালিলিও ছিলেন মূলত গণিতের লোক, ল্যাবরেটরির কাজ সাধারণত করতেন টরিসেলি (ইতালীয় উচ্চারণ টরিচেলি) নামক তাঁর সুযোগ্য সেক্রেটারি। ১৬৪৩ সালে, অর্থাৎ গ্যালিলিওর মৃত্যুর বছর খানেক পর, এই রহস্যের সমাধান খোঁজার চেষ্টায় টরিসেলি একটা লম্বা টিউব জোগাড় করে সেটাকে পারদ দিয়ে ভরে ফেললেন একেবারে কানায় কানায়। তারপর টিউবটিকে উপুড় করে ডোবালেন এক পারদভর্তি পাত্রের ভেতর, যাতে একফোঁটা পারদও বের না হয়ে আসে নল থেকে। তিনি ভাবলেন, যেহেতু নলটি টায়ে টায়ে ভরা, এক কণা বায়ু

টমাস ট্রান্সট্রোমারের পঙক্তিমালার অনুবাদ করেছেন আজীজ রহমান

বেরোবার বা ঢুকবার কোনো পথ নেই, সেহেতু উপুড় অবস্থাতেও ঠিক একই রকম ভরাট অবস্থায় থাকবে নলটি। কিন্তু পরম বিস্ময়ে তিনি দেখলেন, বারবার পরীক্ষা করার পরও, পারার ওপরের দাগটি নল বেয়ে ৩০ ইঞ্চি (৭৬ সেমি) পর্যন্ত উঠছে, তার ওপরে যেতে চাচ্ছে না, বা যেতে পারছে না। তার অর্থ, যেখানে খালি থাকার কথা নয়, সেখানেও খালি সৃষ্টি হয়ে যাচ্ছে আপনা থেকেই। তাহলে সেই ৩০ ইঞ্চির ওপরের জায়গাটুকু কী? কিছুই না। বাতাস ঢুকবার তো কোনো উপায়ই ছিল না, সুতরাং সেটা নিশ্চয়ই শূন্যতায় ভরা, অর্থাৎ ভ্যাকুয়াম! এতে প্রমাণ হয়ে গেল যে প্রকৃতি শূন্যতা পছন্দ না করলেও অপছন্দের একটা সীমা আছে, ঐ ৩০ ইঞ্চি পর্যন্ত, পারাভর্তি নলে, আর ৩৩ ফুট (১০ মিটার) পর্যন্ত পানির টিউবে।

কিন্তু বিজ্ঞানের ধর্মই এমন যে এক সমস্যার সমাধান সাধারণত নতুন সমস্যার বীজ বুনে দেয়। ডেকার্টের চেয়ে ২৭ বছরের ছোট ছিলেন ব্লেই প্যাস্কেল (১৬২৩-৬২) নামক এক তীক্ষ্ণধী ফরাসি বিজ্ঞানী-গাণিতিক। তিনি প্রশ্ন দাঁড় করালেন: ঠিক আছে, বুঝলাম, পানি ওঠে ৩৩ ফুট, আর পারা ওঠে ৩০ ইঞ্চি, কিন্তু কেন? বিষয়টা কী? কী এক খেয়ালের বশে, এক সহকর্মীকে যন্ত্রপাতিসহ পাঠিয়ে দিলেন এক উঁচু পাহাড়ের চূড়ায়। সেখানে ঠিক একই পরীক্ষা করে দেখা গেল, নলের পারদ ৩০ ইঞ্চিও উঠছে না, তার আরো নিচে উঠেই যেন দম হারিয়ে ফেলছে। প্যাস্কেল ভাবলেন, পাহাড়ের বৈশিষ্ট্যটা কী?

কম বায়ুচাপ, সমতলের তুলনায়। তাহলে রহস্যটা নিশ্চয়ই আর কিছুতে নয়, বায়ুচাপে। পাহাড়ে বায়ুর তেমন শক্তি নেই বেশি ওপরে ঠেলার, কিন্তু নিচে চাপ একটু বেশি হওয়াতে পারা বা পানি ঠেলে ওপরে তুলতে অতটা বেগ পেতে হয় না।

যাই হোক, একটা জিনিস তো মীমাংসা হয়ে গেলঃ প্রকৃতির সেই শূন্যভীতির ব্যাপারটি। অবস্থাবিশেষে প্রকৃতি শূন্যকে প্রশ্রয় দেয় বৈকি। সুতরাং অ্যারিস্টটলের শূন্যতত্ত্ব আর পিথাগোরাসের সরলগতি-বিরোধী তত্ত্ব একেবারেই অমূলক। প্রকৃতি যখন যে অবস্থা সে অবস্থাতেই নিজেকে খাপ খাইয়ে নেয়। টরিসেলি আর প্যাস্কেলের পরীক্ষা থেকে এই সিদ্ধান্তটিই যুক্তিসংগত বলে মনে হয়। শূন্য সত্যি সত্যি আছে পৃথিবীতে। ভ্যাকুয়াম কোনো আজগুবি কথা নয়। অন্তত আপাতদৃষ্টিতে।

কয়েক শতাব্দী কেটে গেল তারপর। শূন্য আছে এই বিশ্বাসটি বিজ্ঞানমানসে প্রায় স্থায়ী আসন দখল করে নিয়েছে। ভ্যাকুয়াম টিউবের ব্যবহার আধুনিক প্রযুক্তি জগতের সর্বত্র। তাহলে কি প্রকৃতিতে শূন্যের অস্তিত্ব অবিসংবাদিতভাবে প্রমাণিত হয়ে গেল? হয়তো বা। আবার হয়তো না। আধুনিক বিজ্ঞানে, বিশেষ করে অণুপরমাণুবিষয়ক পদার্থবিজ্ঞানে, এই শূন্যতাবাদী চিন্তাভাবনা একটু নতুন আলোকে পরীক্ষিত হতে শুরু করেছে। কোনো কোনো পণ্ডিত বলছেন: আপাতদৃষ্টিতে যা শূন্য তা আসলে শূন্য নয়, সেখানেও পদার্থ আছে। ঠিক ইন্দ্রিয়গ্রাহ্য পদার্থ হয়তো নয়, কিন্তু পদার্থপদবাচ্য অবশ্যই। কিন্তু সে প্রসঙ্গ এখানে নয়, বরং পরের কোনো অধ্যায়ের জন্য তোলা থাকুক।

ভিন্ন আলোচনায় যাবার আগে ব্লেই প্যাস্কেল সম্বন্ধে দুচারটে মন্তব্য করার লোভ সামলানো যাচ্ছে না। প্যাস্কেলের জন্ম এক প্রচণ্ড রকমের গোঁড়া ক্যাথলিক পরিবারে, অনেকটা ডেকার্টের মতোই। কিন্তু ডেকার্ট পরিবার ছিল জেসুটপন্থী, আর প্যাস্কেলরা ছিল জ্যানসেনবাদী। জ্যানসেনপন্থীরা এতটাই উগ্র মতবাদের ছিলেন যে তাঁরা বিজ্ঞানকে পাপাচার ভাবতেন, বিজ্ঞানসাধনা ছিল শয়তানের অনুগামী হওয়ার শামিল। সৌভাগ্যবশত প্যাস্কেল নিজে ধর্মকর্ম নিয়ে খুব একটা মাথা ঘামাতেন না। বিজ্ঞানচর্চা নিষিদ্ধ জেনেও বেশির ভাগ সময় বিজ্ঞান নিয়েই কাটত তাঁর। প্যাস্কেল ছিলেন এক ক্ষণজন্মা পুরুষ, এত বড় প্রতিভার মানুষ শতাব্দীতে একজন কি দুজন জন্মায় সারা পৃথিবীতে। কৈশোর আর যৌবনে খানিক উচ্ছৃঙ্খলতা হয়তো ছিল তাঁর চরিত্রে। বিজ্ঞানচর্চা থেকে যেটুকু বিরতি পেতেন, সেটুকু তাঁর কাটত জুয়ার আড্ডায়। ভীষণ জুয়ার নেশা ছিল লোকটার। নিজে যে জুয়া খেলতেন তেমন তা নয়, কিন্তু তাঁর অঙ্কের মাথা দিয়ে পেশাদার জুয়ারিদের পরামর্শ দিতেন কখন কোথায় কত টাকা বাজি রাখলে কত লাভ হতে পারে, কত লোকসান। অধিকাংশ ক্ষেত্রে তাঁর পরামর্শ কাজে লেগে যেত। ফলে অত্যন্ত বিত্তশালী জুয়ারিরা টাকার বস্তা নিয়ে তাঁর কাছে ধরনা দিতেন বাজির পরামর্শ নেবার জন্য। এতে প্যাস্কেল নিজে জুয়া না খেলেও প্রচুর ধনসম্পদ করে ফেলেছিলেন। কিন্তু এটা ছিল তাঁর ব্যক্তিগত লাভ। সেটা সাময়িক, অস্থায়ী। চিরস্থায়ী লাভটা হয়েছিল গোটা বিশ্বের।

তাঁর বাজিবিদ্যার সূত্র ধরে কালে কালে একটা নতুন শাখা তৈরি হয়ে যায় গণিতশাস্ত্রের : সম্ভাবনা তত্ত্ব (Probability Theory)। বর্তমান জগতে probability আর statistics-এর ব্যবহার নেই এমন কোনো শাখা বিজ্ঞানে তো নেইই, সমাজবিজ্ঞান, মনোবিজ্ঞান, অর্থনীতি—এধরনের যাবতীয় মূল বিজ্ঞানবহির্ভূত বিষয়েও এর ব্যবহার প্রায় অপরিহার্য হয়ে দাঁড়িয়েছে। ভাবতে অবাক লাগে যে জুয়ার মতো একটি খারাপ নেশা, যার প্রতি ধর্ম এবং সমাজ দুটিরই বিরূপ দৃষ্টি, সেই ঘৃণিত জিনিসটি থেকেই উৎপন্ন হয়েছে জ্ঞানবিজ্ঞানের অত্যন্ত গুরুত্বপূর্ণ একটি শাখা, এবং সপ্তদশ শতাব্দীর এই পথভ্রষ্ট উচ্ছৃঙ্খল যুবক তার আদি জনক (যদিও এই জনকত্বের অংশীদার হিসেবে গেলার্মো কার্ডানো এবং পিয়ের ফার্মার নামও উল্লেখ করা হয়)। আমার (মী.র) ব্যক্তিগত মত: সম্ভাবনাতত্ত্বের আবিষ্কার অনেকটা অভিকর্ষ তত্ত্বের মতোই এক যুগান্তকারী, মৌলিক আবিষ্কার। প্রকৃতির অন্যান্য মৌলিক সত্যের মতো সম্ভাবনাও একটি মৌলিক সত্য, আমার বিচারে।

প্যাস্কেলের গল্প অবশ্য এখানেই শেষ হয়ে যায় না। ১৬৫৪ সালের ২৩ নভেম্বর। তাঁর জীবনের সবচেয়ে স্মরণীয় দিন। পুরাকালের পয়গম্বররা যেমন দৈববাণী বা অহি লাভ করতেন হঠাৎ হঠাৎ, তেমনি প্যাস্কেলেরও এক অতি- প্রাকৃতিক অভিজ্ঞতা হয়ে গেল সেদিন। কোথা থেকে এক ঐশী বাণী এসে তাঁর জীবনের মোড় আগাগোড়া বদলে দিল এক রাতের মাঝে। ধর্মকর্মে পরম উদাসীন মানুষটি হঠাৎ পরম ধার্মিক হয়ে উঠলেন। গণিত, জুয়া, বিজ্ঞান সব ছেড়েছুড়ে সাধু-ব্রত গ্রহণ করলেন পরের দিন থেকে। একেবারে ভিন্ন মানুষ। ৩১ বছর বয়সে প্যাস্কেল ফিরে গেলেন তাঁর পৈতৃক ধর্মচর্চায়।

কিন্তু ঐশী বাণী হলে কী হবে, সহজাত মেধা যাবে কোথায়। কৌতূহল আর অনুসন্ধিৎসা যার রক্ত-মজ্জায় তাকে ধর্মের তাবিজ দিয়ে বশ মানানো কি সম্ভব? ধর্ম তাঁর একপ্রকারের অস্থিরতা কমাতে সক্ষম হলেও বুদ্ধির অস্থিরতা অন্যরকমের অশান্তির ঝড় তুলল মনে। চার বছর পর একটা শক্ত অসুখ হলো তাঁর। তখন তিনি জ্ঞাতসারেই প্রভুর কাছে কিছুদিনের জন্য ছুটি কামনা করে জ্ঞানসাধনায় মনোযোগ দিলেন। ঠিক বিজ্ঞান না হলেও বিজ্ঞানসংক্রান্ত, সাথে সাথে ধর্মবিষয়কও। ভাবলেন, তাহলে নিশ্চয়ই মহাপ্রভু ক্ষমার দৃষ্টিতেই দেখবেন তাঁর কর্মকাণ্ডকে। ঠিক করলেন, জুয়ার বাজিতত্ত্ব দিয়েই তিনি ঈশ্বরের অস্তিত্ব প্রতিষ্ঠা করবেন। ঈশ্বর বিশ্বাস করাতে কত ঝুঁকি আর না করাতে কত ঝুঁকি তার একটা আনুমানিক সংখ্যা দাঁড় করিয়ে তিনি সিদ্ধান্তে পৌঁছালেন যে বিশ্বাস করাটাই কম ঝুঁকিপূর্ণ, না করাতে বিস্তর বিপদের আশঙ্কা। রীতিমতো অঙ্ক কষে বের করা সব ফলাফল, যদিও অঙ্কটা কিভাবে করা হলো, কী ধ্যানধারণার ভিত্তিতে সে বিষয়ে আধুনিক চিন্তাবিদদের কিছু প্রশ্ন থাকতে পারে বৈকি। প্যাস্কেলের যুক্তি ছিল অনেকটা এরকমঃ ধরুন, খোদা আছে। তাহলে তাঁকে বিশ্বাস করাতে ‘অসীম’ ফায়দা। তিনি যদি না থাকেন তাহলে বিশ্বাস করে লাভ বা লোকসান কোনোটাই নেই, তার অর্থ ‘শূন্য’ ফায়দা। আর যদি খোদা থাকেন এবং তা সত্ত্বেও বিশ্বাস করা হচ্ছে না তাহলে তার শাস্তি গুরুতর, অর্থাৎ ‘অসীম’ বিপদ। তবে তিনি না থাকলে বিশ্বাস বা অবিশ্বাস তাতে কিছু আসে যায় না। মোটমাট তাঁর হিসাব মতে বিশ্বাস স্থাপন করাটাই বুদ্ধিমানের কাজ, এতে কোনো ঝুঁকি নেই। পাকা ধার্মিকের যুক্তি হয়তো নয় এটা, তবে পাকা জুয়ারির যুক্তি তাতে সন্দেহ নেই। জুয়ারির যুক্তি দিয়ে তিনি একাধারে শূন্য, অসীম ও ঈশ্বরের অস্তিত্ব প্রমাণ করে ফেললেন। অবশ্য সেই যুক্তিতেও বেশ কিছু ফাঁক আছে, সেটা পরবর্তী কালের যুক্তিবাদীরা চোখে আঙুল দিয়ে দেখিয়ে দিয়েছিলেন। এই বইয়ের লেখকদের একজন (অ.রা) এ নিয়ে মুক্তমনায় একটি বিস্তৃত পোস্ট লিখেছিলেন ঈশ্বরের অস্তিত্ব প্রমাণে প্যাস্কেলের বাজির অসারতা নিয়ে। ২০১২ সালের জুন মাসে মুক্তমনায় প্রকাশিত লেখাটির শিরোনাম ছিল –‘প্যাস্কেলের ওয়েজার——আস্তিক হওয়াটাই কি একমাত্র নিরাপদ বাজি?”

ব্লেই প্যাস্কেলের বর্ণাঢ্য জীবনের বিচিত্র কাহিনি বিস্তৃতভাবে জানবার আগ্রহ থাকলে পাঠককে তাঁর পূর্ণ জীবনী পড়তে হবে।

অভিজিৎ রায়, প্যাস্কেলের ওয়েজার—আস্তিক হওয়াটাই কি একমাত্র নিরাপদ বাজি?, মুক্তমনা, জুন ২৮, ২০১২

জেনোর ধাঁধা ফিরে এল

এবার কিছুক্ষণের জন্য জেনোর ধাঁধাতে ফিরে যাব আমরা। ধাঁধাটির সূত্রপাত কোথায় সে ইঙ্গিত তো আগেই দিয়েছি। সেকালের পণ্ডিতরা বুঝতে পারছিলেন না

1,1/ 2,1/ 4,1/8,….,1/2ⁿ,….

এই যে অন্তহীন সংখ্যামালা, এগুলো তো যাচ্ছে না কোথাও, এদের কোনো গন্তব্য নেই। শুধু তা-ই নয়, এগুলোকে যোগ করলে দাঁড়ায় আরেক অদ্ভুত জিনিসঃ

1+1/2+1/22 +1/23 +…+1/2ⁿ +…..

এরই বা শেষ কোথায়? অন্তহীন সংখ্যার যোগফল তো অন্তহীন হবারই কথা, তাই না?

আমরা যেন ভুলে না যাই যে যুগটা ছিল যিশুখ্রিষ্টের জন্মের দু-চার শ বছর আগে। এবং সমাজটি ছিল এমন যে বড় বড় পণ্ডিতরাও ভাবতেন, ‘শূন্য’ আর ‘অসীম’ দুটোই অমঙ্গলের সহোদর, দুষ্ট লোকের কল্পনাতেই আশ্রয় পায় তারা, বাস্তবে নয়।

এই দুটি প্রশ্নকেই একটু উল্টেপাল্টে পরীক্ষা করা যাক। জেনোর ধাঁধাতে ১/২ একটি বিশেষ সংখ্যা। এটি ১/২ না হয়ে ১/৩ বা ১/৫ হতে পারত, কিংবা অন্য যেকোনো ভগ্নাংশ, যার মান ১-এর কম, 0 -এর বেশি। সার্বজনীনতার খাতিরে বরং ধরা যাক

1,x,x², x³,….,xⁿ, …,

যেখানে x একটি সাংকেতিক সংখ্যা, যার মান শূন্য থেকে একের মাঝে। ‘অসীম’ নিয়ে যেহেতু কিঞ্চিৎ সমস্যা আছে আমাদের, সেহেতু n -সংখ্যক সংখ্যা নিয়ে আমরা অসীম পর্যন্ত না গিয়ে

1+x+x² + x³ + …..+x^(n-a) (১)

এই সীমিত রাশিটির যোগফল বের করার চেষ্টা করব। ছোটবেলার স্কুলে পড়া বিদ্যা দিয়েই আমরা অনায়াসে বুঝে ফেলতে পারছি যে সংখ্যাগুলো পরস্পরের সঙ্গে একটা গুণোত্তর প্রগতিসূত্রে বাঁধা। এধরনের গুণোত্তর রাশি নতুন কিছু নয়। ব্যাবিলনীয়রা দুহাজার বছর আগেই এরকম রাশি নিয়ে চিন্তাভাবনা করেছিলেন। মিসরের ‘আহমেস প্যাপিরাস’ (আ. ১৫৫০ খ্রি.পূ.) নামক গণিতগ্রন্থে একটি গুণোত্তর রাশির বর্ণনা পাওয়া যায়। মজার ব্যাপার হলো যে আহমেসে যে পদ্ধতি দেওয়া আছে, প্রায় একই পদ্ধতি ব্যবহার করেছিলেন ইতালির ফিবোনাচি তাঁর ১২০২ সালের গ্রন্থটিতে। আরকিমেডিস (আ. ২২৫ খ্রি.পূ.) নিজেও একটি অধিবৃত্তের ক্ষেত্রফল বের করতে গিয়ে (১)-এর মতো রাশি ব্যবহার করেছিলেন, যাতে x -এর মান ছিল ১/৪।

n যদি ছোট হয়, তাহলে হাতে গুণেই ফলাফল বের করে ফেলা যায় রাশিটির যোগফল। কিন্তু গাণিতিকেরা হলেন কুঁড়ে প্রকৃতির লোক, সব সময়ই একটা সহজ পথ বের করার তালে থাকেন। এই সহজ পন্থা বা চালাকিটির গাণিতিক নাম হলো ‘ফর্মুলা’ বা আর্যা। দেখা যাক ওপরের (১)-এর জন্য এমন একটি আর্যা বের করা যায় কি না। প্রথমত x =0 হলে ওপরের সব x শূন্য হয়ে থাকে কেবল প্রথম সংখ্যাটি, অর্থাৎ ১। এবার ধরুন x=1. তাহলে সব সংখ্যাই ১-এর সমান। যেহেতু সর্বমোট সংখ্যা হলো n, সেহেতু তার যোগফলও n.

এবার মনে করুন x শূন্য বা ১ কোনোটাই নয়। তাহলে কী হবে? সুবিধার জন্য রাশিটির একটা নাম দেওয়া যাক, ধরুন S(x)। (বন্ধনীর ভেতরে x বেচারিকে আটকে ফেলার উদ্দেশ্য হলোx-এর মান বদলালে যে S-এর মানও বদলাতে বাধ্য, সেটাই পরিষ্কার করে লিখে দেওয়া) এখন আমরা ওপরের রাশিটিকে নতুন করে লিখবঃ

S(x) = 1 + x + x² + ….+ x^(n-1)(২)

এবার দুধারে x দিয়ে গুণ করলে দাঁড়ায়

xS (x) = x + x²+……+ x^(n-1) + xⁿ(৩)

এ পর্যায়ে আমরা (২) থেকে (৩) বিয়োগ করব। ডান দিকে x থেকে x(n-1) পর্যন্ত ওপরে-নিচে কাটাকুটি হয়ে বাকি থাকে কেবল ১ আর একেবারে শেষেরটি, xn,সুতরাং ফল দাঁড়াচ্ছেঃ

(1 − x)S(x) = 1−xⁿ . (৪)

উদ্দিষ্ট লক্ষ্যে প্রায় পৌঁছে গেছি আমরা। বাকি রইল কেবল ( 1 − x ) দিয়ে ভাগ করা দুদিকে। (ভাগ করা কাজটি কিন্তু ভেবেচিন্তে করা দরকার, সেটা নিশ্চয়ই মনে আছে পাঠকের)। যা-ই হোক আপাতত ওসব জটিল চিন্তায় না গিয়ে সোজা হিসেবে দেখা যাচ্ছেঃ

S(x) = (1-xⁿ)/(1-x). (৫)

অলস গাণিতিকের জন্য একটি শিশুবোধ দাওয়াই বা ফর্মুলা বেরিয়ে গেল; কষ্ট করে এতগুলো সংখ্যা যোগ করবার প্রয়োজন নেই, (৫)-এর কল্যাণে চট্ করে সেরে ফেলা যায় কাজটি। যেমন ধরুন, জেনোর ধাঁধার ক্ষেত্রে X হলো ১/২। তাহলে

S (1/2) = (1 − 1 / 2ⁿ ) /( 1 − 1 / 2 ) = 2 (1 − 1/2ⁿ ) (৬)

আরকিমেডিসের বেলায় x = 1/4 . সেক্ষেত্রে

S(1/4) = 4/3(1 − 1/4ⁿ) .

দশ বছরের বাচ্চাও বেশ মজা পেয়ে উঠবে। তবে দশ বছরের বাচ্চা হয়তো যেটা ভাববে না সেটা এক মৌলিক প্রশ্নঃ

(৪) নম্বর সূত্রটি কি সবক্ষেত্রে প্রযোজ্য? না, তা নয়। অন্তত সোজা পূরণ-ভাগের ব্যাপার নয় সেটা। প্রথমত দেখা যাক x এর মান 0 আর ১ থেকে কী পাই আমরা।

S(0) = 1/1=1,

যা মিলে যাচ্ছে আগেকার পাওয়া ফলাফলের সঙ্গে। এবার x=1 বসানো যাক। (৪) দিচ্ছে0/0, যার কোনো অর্থ নেই। অথচ (১) আর (২) থেকে সোজা হিসাব করেই আমরা পেয়েছিলাম _S(1) = n. তাহলে কি বোঝায় 0/0 আর n এক জিনিস? না, তাই বা হয় কিভাবে? n তো যেকোনো পূর্ণ সংখ্যা হতে পারে। তার অর্থ 0/0 ভগ্নাংশটির কোনো নির্দিষ্ট মান নেই, যা আমরা আগেও উল্লেখ করেছিলাম একবার। এ এক ধাঁধা বটে।

এর পূর্ণ সমাধান পেতে অনেক অনেক শতাব্দী অপেক্ষা করতে হয়েছিল গণিতজগৎকে। এর মূলে আছে সেই শূন্য দিয়ে ভাগ করবার নিষিদ্ধ ব্যাপারটি। x যদি 1 হয়, 1−x তাহলে শূন্য হবে, এবং সেটা দিয়ে (৪)-এর দুপাশে ভাগ করা রীতিমতো বেআইনি। এই ডামাডোল থেকে আমাদের উদ্ধার করে দিয়েছে নিউটন আর লিবনিজের আবিষ্কৃত নতুন শাস্ত্র ক্যালকুলাস। তবে এদুই মহারথীর কেউই ঠিক 0/0-এর রহস্য উদ্ঘাটন করতে পারেননি; সেটা করেছিলেন সপ্তদশ শতাব্দীর গাণিতিক জ্যা বার্নলি (১৬৬৭-১৭৪৮) [যদিও এর কৃতিত্ব নিয়েছিলেন ফ্রান্সের আরেক কৃতি গাণিতিক লোপিতাল (১৬৬১-১৭০৪), এবং বিশ্ববিদ্যালয়ের পাঠ্যপুস্তকে সে নামেই পরিচিত এই জনপ্রিয় সূত্রটি]। সে প্রসঙ্গে আমরা যাব ক্যালকুলাসের মূল বিষয়গুলো নিয়ে একটু আলাপ-আলোচনার পর।

আচ্ছা, x যদি 0 আর ১-এর মধ্যে কোনো সংখ্যা হয় তাহলে xⁿ -এর মান কী দাঁড়ায়? মনে করুন, x =১/৩। তাহলে ১/৩² =১/৯, ১/৩³ =১/২৭, ১/৩⁴ =১/৮১, ১/৩⁵ = ১/২৪৩,…, অর্থাৎ দ্রুত ছোট হয়ে যাচ্ছে এর মান, n -এর মান যত বাড়ছে। সুতরাং n যদি লক্ষকোটি বা তারও বেশি কোনো সংখ্যা হয় তাহলে ভগ্নাংশটির কী দশা হবে? একেবারে তুচ্ছ, তাই না? যাকে অঙ্কের ভাষায় বলা যায় নগণ্য, negligible. এই যে n বেড়ে বেড়ে অসীমের দিকে ছোটা আর সাথে সাথে xⁿ -এর মান কমে কমে শূন্যের দিকে ছোটা, এর মধ্যেই চুপিসারে এসে যাচ্ছে সেই ‘শূন্য’ আর ‘অসীম’-এর ব্যাপারটি। শুধু তা-ই নয়, আরো একটি বড় আইডিয়ার অঙ্কুর গজিয়ে উঠছে, যাকে গণিতের ভাষায় বলা হয় লিমিট (limit). ভাসাভাসাভাবে আমরা এখনি বলে দিতে পারি যে n যখন অসীম লিমিটে যায়, xⁿ তখন যায় (0) লিমিটে। সাংকেতিক ভাষায় এটাকেই আমরা লিখি এভাবেঃ

lim_{n→ ∞} x = 0,

অর্থাৎ যখন । যায় অসীম লিমিটে। অবশ্য তার জন্য শর্ত দরকার যে x – কে একটি সত্যিকার ভগ্নাংশ হতে হবে, মানে তার মান যেন ১-এর কম হয়। এই ‘কম হওয়া’ ব্যাপারটিকে আমরা ‘<‘ চিহ্ন দিয়ে নির্দেশিত করি। বেশি হওয়াকে লিখি ‘>’ চিহ্নের সাহায্যে। সুতরাং 0 < x < 1 হলে

lim_{n→ ∞} S(x)=1/(1-x),

যখন n যায় অসীম লিমিটে।

জেনোর ধাঁধার বেলায় যেহেতু x-এর মান ১/২, সেহেতু S(1/2)-এর লিমিট হলো ১/(১-১/২) অর্থাৎ ২, অসীম নয়। সুতরাং ‘অসীম’সংখ্যক ধাপ অতিক্রম করতে হলেও খরগোশকে অসীম দূরত্বে যেতে হয় না, বা অসীম সময় ক্ষেপণ করতে হয় না, এক লাফেই পার হয়ে যায় দুই একক সময়ের মধ্যে—মাত্র তো ২ ফুট, ২ গজ বা ২ সেকেন্ড বা ২ মিনিটের ব্যাপার। এই সামান্য ঘটনাটি সেকালের মহা মহা পণ্ডিতদের মাথায় ঢোকেনি, যার একটাই কারণ, শূন্য আর অসীমের অস্তিত্ব নিয়ে সমস্যা, এবং লিমিটের কোনো ধারণা না থাকা।

অথচ কাজে কর্মে কিন্তু লিমিট বারবারই উঁকি মারছিল পুরাকালের গবেষকদের মস্তিষ্কে। সে গল্প করব পরবর্তী অধ্যায়ে। আপাতত শূন্য আর অসীম নিয়ে আরো কিছু সময় কাটানো যাক। ওপরের আলোচনা থেকে এটা বোঝা যাচ্ছে যে

S(x)=1+x+x² + .+xⁿ +….. (৭)

যদি দিগদিগন্ত পার হয়ে অসীম পারাপারে চলে যায়, তাহলেও এর একটা সীমিত মান আছে, 1/(1 − x), যার অর্থ দাঁড়ায়ঃ

S(x) = 1/(1-x). (৮)

এই উদাহরণ থেকে পাঠক যেন ভেবে না বসেন যে ১-এর চেয়ে কম এরকম অসীমসংখ্যক সংখ্যার সব যোগফলই সীমার মধ্যে থাকবে। যেমন,

১+১/২+১/৩+১/৪+…. (৯)

এই সহজ রাশিটি অসীমের দিকে যাচ্ছে ঠিকই, এবং সংখ্যাগুলোর মানও ছোট হতে হতে শূন্য হয়ে যাচ্ছে, কিন্তু তা সত্ত্বেও এটি কোনো সসীম সংখ্যায় পৌঁছুচ্ছে না, বরং যাচ্ছে অসীমেরই দিকে। ক্যালকুলাসের ছাত্রদের যেটা শিখতে হয় সেটা হলো যে অসীম রাশির সংখ্যাগুলো ক্রমান্বয়ে ছোট হয়ে যাওয়াটাই যথেষ্ট নয়, কত দ্রুত ছোট হচ্ছে সেটাই হলো আসল প্রশ্ন। গুণোত্তর রাশির বেলায় সে হারটি যথেষ্ট দ্রুত বলেই (৭) থেকে (৮) পর্যন্ত পৌঁছানো সম্ভব হলো, কিন্তু (৯)-এর বেলায় তা পারা গেল না, কারণ ১,১/২,১/৩,… এ সংখ্যাগুলোর শূন্যে যাওয়ার গতিটা বড় ঢিলে।

অসীমসংখ্যক সংখ্যার যোগফল নিয়ে কাজ করার আরো অনেক বিড়ম্বনা আছে। সংখ্যাগুলো যদি সব ধনাত্মক হয়, বা সব ঋণাত্মক, তবু খানিক রক্ষা, মিশ্রিত হলে তো সেরেছে। যেমন ধরুনঃ

১-১+১-১+১-১+…. (১০)

এর যোগফল কী হবে? আদৌ কোনো যোগফল আছে কি না? প্রথম দৃষ্টিতে মনে হবে, এতে ভাববার কী আছে? (১০)-এর প্রথম জোড়ার যোগফল ০, দ্বিতীয় জোড়া, তৃতীয় জোড়া, চতুর্থ, পঞ্চম,…, এভাবে যেতে যেতে পরিষ্কার দেখা যাচ্ছে সব জোড়া থেকে একই ফল পাচ্ছি আমরা: শূন্য। অর্থাৎ,

(১-১)+(১-১)+(১-১)+….= 0. (১১)

এতে ভুলের কী আছে? কিন্তু না, এত সহজে ছাড় পাবেন না। বন্ধনীগুলোকে (১১)-এর মতো করে না সাজিয়ে একটু অন্যভাবে সাজানো যাক। যেমন —

১-(১-১)-(১-১)-(১-১)-… (১২)

এখন কী দেখছি আমরা? সবগুলো বন্ধনীবদ্ধ সংখ্যাদ্বয় কাটাকুটি করে শূন্য হয়ে যাচ্ছে, থাকছে শুধু প্রথম সংখ্যাটি, অর্থাৎ ১। সুতরাং (১২)-এর যোগফল মনে হচ্ছে ১। কিন্তু একটু আগেই তো দেখলাম যোগফল শূন্য। শূন্য আর ১ এক হয় কী করে? কোনটা সত্য? সত্য হলো যে কোনোটাই সত্য নয়, আবার দুটোই সত্য। তার অর্থ এধরনের যোগ-বিয়োগযুক্ত রাশি বড়ই ঝামেলা সৃষ্টি করে। বড় বড় মাথাওয়ালা ব্যক্তিদেরও মাথা ঘামিয়ে ফেলে। সুতরাং সে প্রসঙ্গ এখানেই শেষ করব। এগুলো শিখবার জায়গা প্রথম বর্ষের ক্যালকুলাস নয়, তারও এক ধাপ ওপরের কোর্স, যাকে বলা হয় রিয়েল অ্যানালিসিস, বেশ জটিল বিষয়, সেখানে ঢুকতে হবে।

লিমিটের ছলাকলা

আমার (মী.র) ছাত্রজীবনে ক্যালকুলাস শেখা শুরু হয়েছিল বিশ্ববিদ্যালয়ের প্রথম বর্ষে। বিসমিল্লাতেই যে জিনিসটা শিখতে হয়েছিল আমাদের সেটা হলো লিমিট, কারণ লিমিটই হলো ক্যালকুলাসের ভিত্তি। প্রথম সংজ্ঞাটিই বর্ণনা দেয় লিমিট কাকে বলে। একে এড়ানোর কোনো উপায় নেই। প্রকৌশল আর ফলিত বিজ্ঞানের ছাত্ররা লিমিট পছন্দ করে না (তারা মনে করে, এটা অনর্থক সময় নষ্ট করা মাত্র), ডাক্তাররা ভাবে, এটা অনাবশ্যক, কলার ছাত্রদের মনোভাব, লিমিট একটি রসকষহীন শুষ্ক বিষয় যা মানবচিত্তের বিকাশ সাধনে বিন্দুমাত্র সহায়তা করে না। আর প্রথম বর্ষের গণিত ছাত্ররা? বেচারিদের কোনো গত্যন্তর নেই। পড়েছি মোগলের হাতে, খানা অবশ্যই খেতে হবে সাথে। আক্কেল হারিয়েছিলাম বলেই তো অঙ্কতে অনার্স নেওয়া, এখন তিতে ওষুধটা আগেভাগে গিলে ফেলাই ভাল। তাই আমরা গিলে ফেলতাম। চোখ বুজে। মনে পড়ে না আমি (মী.র) বা আমার সহপাঠীদের এমন কেউ ছিল যে হলপ করে বলতে পারত সে সত্যি সত্যি বুঝেছিল লিমিট জিনিসটা আসলে কী। মুখস্থ করা এক জিনিস আর সত্যি সত্যি বুঝে ফেলা আরেক জিনিস। এমনিতেই আমাদের দেশে বোঝার চেয়ে পড়া আর মুখস্থের ওপরই জোর বেশি, তার ওপর লিমিটের মতো একটি দুরূহ বিষয় যা নিয়ে পুরাকালের বড় বড় পণ্ডিতদেরও মাথার তালু দিয়ে ধোঁয়া ছুটত। আমি (মী.র) সারা জীবন অঙ্ক পড়িয়েছি-ক্যালকুলাস আর লিমিট পড়িয়েছি অসংখ্যবার। অথচ এই আমিও লিমিট ব্যাপারটা অনার্সের একেবারে শেষ পরীক্ষার আগ পর্যন্ত ঠিক বুঝিনি। যন্ত্রের মতো অঙ্ক কষে যেতে পারতাম, কিন্তু কোনো আনাড়ি মানুষকে সহজ ভাষায় বোঝানো যায় এমন করে বুঝিনি। ‘ভালো করে শেখা’ বলতে এই বুঝি আমি—এটাই বুদ্ধির পরীক্ষা—রাস্তার মানুষকে রাস্তার ভাষাতেই জটিল একটা বিষয় ব্যাখ্যা করে বোঝাতে পারা, সেটাই পাণ্ডিত্যের লক্ষণ। সেই শেখাটুকু আমার শেখা হয়েছে ক্যানাডায় শিক্ষকতা শুরু করার বেশ কিছু পরে।

কিন্তু কেন? কেন লিমিটকে ঘিরে এত রহস্য? মিথ্যে প্রবঞ্চনায় বারবার কেন বিভ্রান্ত করা মেধাবী-অমেধাবী সবাইকে সমানভাবে? প্রথম কারণ, এতে ‘শূন্য’ দেখা দেয় খেলার সঙ্গী হবার জন্য, ধরা দেওয়ার জন্য নয়। সে এসেও ধরা দিতে চায় না। এখানে ‘শূন্য’ আসে 0/0_এর ভয়ংকরী মূর্তি নিয়ে, অথচ পুরোপুরি তা-ও নয়। এ এক অদ্ভুত জিনিস। ‘শূন্যের’ কাছে যাব, অতি কাছে, যত কাছে তোমার কল্পনায় আসে তত কাছে, তবু ঠিক শূন্যের গায়ে উপুড় হয়ে পড়ব না। প্রিয় তোমার সঙ্গটুকু দাও শুধু, ছোঁয়াটুকু নয়, এই যেন লিমিটের কামনা।

ছোট্ট একটা উদাহরণ দিই। ভারতীয় গাণিতিক ভাস্কর তাঁর স্বদেশি ব্রহ্মগুপ্তের ভুল সংশোধন করে বলেছিলেন, সঠিকভাবেই, যে ১/০ বা (১৫৫৫৬)/০-জাতীয় ভগ্নাংশের মান হলো অসীম। কিন্তু ধরুন কোনো বিশেষ সংখ্যার উল্লেখ না করে আমরা চাচ্ছি, x সূচক একটি সংখ্যা শূন্যের দিকে অগ্রসর হলে, 1/x, এই ভগ্নাংশটি কোন পথে ধাবিত হবে তা জানতে। অর্থাৎ

lim _{n→ ∞}(1/x) = ? (১৩)

এক মুহূর্ত অমনোযোগী হলেই কিন্তু ফাঁদে পড়ে যাবেন, বলবেন, কেন, এটা তো পরিষ্কারই দেখা যাচ্ছে অসীম। ১/০ যদি অসীম হয় তাহলে ওপরের লিমিটটি অসীম হবে না কেন? বলছি না যে আপনি ভুল বলছেন; না, ভুল নয়, আংশিক ভুল। অসীম বলতে সাধারণভাবে আমরা বুঝি অসীম বড় কোনো সংখ্যা, অর্থাৎ ধনাত্মক অসীম। সেটা ঠিক, যদি (১৩)-এর লিমিটটিতে x শূন্যের দিকে যায় ডান দিক থেকে, যার অর্থ ধনাত্মক দিক থেকে। কিন্তু লিমিট বলতে তো ডান দিক বাঁ দিক উভয় দিক বোঝাতে পারে। বাঁ দিক থেকে যদি x আসে শূন্যের দিকে তাহলে তো এটা ধনাত্মক অসীম থাকছে না, থাকছে ঋণাত্মক অসীম। এ থেকে কী সিদ্ধান্তে পৌছুব আমরা? দুটো লিমিটই ঠিক? না, তা নয়। এখানে সঠিক সিদ্ধান্ত হলো যে ওপরের লিমিটটির আসলে কোনো অস্তিত্বই নেই। এই যে লিমিটের অস্তিত্ব থাকা বা না থাকা, এর ওপরই গা ছড়িয়ে আছে অ্যানালিসিস শাখাটির অঙ্গ-প্রত্যঙ্গ, যার প্রাথমিক পর্যায়ের নাম হলো ক্যালকুলাস।

ক্যালকুলাসের একেবারে গোড়াতে যে আইডিয়াটি সেটা হলো ‘ক্ষুদ্র সংখ্যা’। ইংরেজিতে যাকে বলা হয় infinitesimal. সেই যে বললাম, শূন্যের নিকটতম প্রতিবেশী অথচ শূন্য নয়, যা চালাক মানুষকেও বোকা বানিয়ে ফেলে। বেশ কয়েক শতাব্দী ধরে মানুষ এই আইডিয়াটি নিয়ে হিমশিম খেয়েছে। এটা নিয়ে কাজ করেছে, ব্যবহার করেছে দৈনন্দিন প্রয়োজনে, কিন্তু স্পর্শ করতে সাহস পায়নি। গরম লোহার মতো, যা না হলে দা-কুড়াল বানানো যায় না, অথচ ছোঁয়া মানে নির্ঘাত হাত পোড়ানো।

‘ক্ষুদ্র সংখ্যা’র ব্যবহার আজকের নয়, পুরাকাল থেকেই।

দৈনন্দিন জীবনে ক্যালকুলাস

ব্যবহারিক প্রয়োজন বলতে কী বোঝায়? আহার্য। পরিধেয়। আলোবাতাস, জল, বৃষ্টি। বাসগৃহ। জমিজমা। জমিজমার মাপজোক করতে হয়। গৃহের দৈর্ঘ্য-প্রস্থ মাপতে হয়। প্রাচীন মিসরীয়রা সেভাবেই জ্যামিতি আবিষ্কার করেছিলেন। সেভাবেই তাঁরা প্রথম সূচনা করেছিলেন সরলরেখা, সমতল, ত্রিভুজ, চতুর্ভুজ, কোণ, সমকোণ, এসব শব্দ। একই সময় চীন, ভারতবর্ষ এবং অন্যান্য জাতির চিন্তাবিদদের মাথায় অনুরূপ ভাবনা জেগে থাকতে পারে, তার কোনো লিপিবদ্ধ ইতিহাস আমাদের জানা নেই। সরলরেখার দৈর্ঘ্য বলতে কী বোঝায় সেটা আমরা জানি, একটা পাঁচ বছরের শিশুও সেটা বোঝে। দৈর্ঘ্য মাপার জন্য আছে মানদণ্ড (রুলার)। আমেরিকায় ইঞ্চি, ফুট, গজ, ইত্যাদি, ক্যানাডা-ইউরোপে মিটার- সেন্টিমিটার-কিলোমিটার। অবশ্য দৈর্ঘ্য বলতে কী বোঝায় সে-ও এক মৌলিক প্রশ্ন। সক্রেটিস হলে হয়তো বলতেন, দৈর্ঘ্য মাপার আগে বাপু, আমাকে বুঝিয়ে দাও ‘দৈর্ঘ্য’ শব্দটার অর্থ কী। বর্তমান যুগের বিশুদ্ধতাবাদী তাত্ত্বিক গাণিতিকেরা (pure mathematicians) বলবেনঃ দৈর্ঘ্য? কিসের দৈর্ঘ্য? সেট (set) টা কী? ওটা কি ফাঁকা ফাঁকা, না একটানা (discrete or continuous)? পরিমাপনীয় (measurable), না অপরিমাপনীয়? সেসব প্রশ্নের উত্তর দিতে আপনার ত্রাহি ত্রাহি অবস্থা দাঁড়াবে। বিশুদ্ধ গাণিতিকেরা বড় খুঁতখুঁতে জাতি, আগেকার দিনের দার্শনিকদের মতো। যুক্তির শক্ত গাঁথুনিতে বাঁধা না হলে কিছুতেই তাদের তুষ্টি হয় না। আপাতত আমরা সেই যুক্তিযুদ্ধ থেকে দূরত্ব বজায় রাখব।

আলোচনার সুবিধার জন্য দু-চারটে তথ্য আমরা স্বতঃসিদ্ধ বলে ধরে নেব, বিশেষ করে ইউক্লিডের বইতে যেসব তথ্য দেওয়া আছে, ধরে নেব যে সেগুলো বিনা প্রশ্নেই মেনে নেওয়া যায়। তাহলে একটা সমকোণী চতুর্ভুজের ক্ষেত্রফল হলো তার ‘দৈর্ঘ্য’ ও ‘প্রস্থে’র গুণফল। (লক্ষ করুন যে দৈর্ঘ্য ও প্রস্থ দুটি শব্দতেই চিহ্ন ব্যবহার করা হয়েছে। তার কারণ চতুর্ভুজের কোন বাহুটা তার দৈর্ঘ্য, কোনটি প্রস্থ, সেটা নেহাতই দর্শকের দৃষ্টিভঙ্গির ওপর নির্ভর করে)। আমরা এ-ও ধরে নেব যে একটা ত্রিভুজের ক্ষেত্রফল হলো তার দৈর্ঘ্য ও প্রস্থের গুণফলের অর্ধেক। এই সামান্য দু-তিনটে তথ্য জানা থাকলেই এক আশ্চর্য উপায়ে ক্যালকুলাসের দুটি মুখ্য শাখা, অন্তরকলন (differential calculus), এবং সমাকলন (integral calculus), তাদের একটা প্রাথমিক ধারণা দাঁড় করানো সম্ভব। এ দুয়ের মাঝেই চুপটি করে লুকিয়ে আছে ‘শূন্য’ আর 0/0-জাতীয় অনির্ণেয় সংখ্যার বীজ।

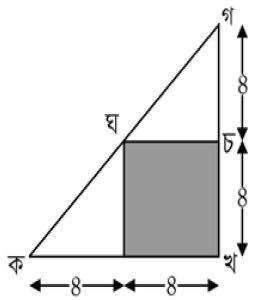
ধরুন একটি সমদ্বিবাহু (isosceles) ও সমকোণী (right-angle) ত্রিভুজ, যার দৈর্ঘ্য-লম্ব দুই-ই ৮ সেন্টিমিটার। ভূমিতে ক হলো এক কোনায়, খ আরেক কোনায়, আর গ হল লম্বের মাথায়। অর্থাৎ ক থেকে গ রেখাটি ত্রিভুজের অতিভুজ। ইউক্লিডের জ্যামিতি থেকে আমরা জানি,এর ক্ষেত্রফল হলো (৮×৮)/২=৩২ বর্গসেন্টিমিটার।

এখন এক কাজ করা যাক। ভূমির ঠিক মধ্যিখানে, অর্থাৎ ক থেকে চার একক দূরত্বে যে বিন্দুটি সেখান থেকে একটা লম্ব আঁকা যাক যেটা মিশছে, ধরুন, অতিভুজ কগ রেখাটির ঘ বিন্দুতে। ঘ থেকে ভূমির সমান্তরাল একটি রেখা আঁকুন খগ অবধি। এটা মনে করুন চ বিন্দুতে মিশল। এভাবে গঠিত যে বর্গক্ষেত্রটি পেলাম আমরা তার ক্ষেত্রফল কত? ৪×৪=১৬, সোজা হিসাব। পুরো ত্রিভুজটির অর্ধেক।

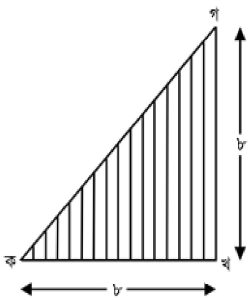
আন্দাজ হিসেবে চলনসই, কিন্তু খুব সূক্ষ্ম আন্দাজ নয়। তার চেয়ে ভালো অনুমান পেতে হলে ভূমিতে আরো বেশি খণ্ড বিন্দু নিতে হবে। দুভাগ না করে সমান করে যদি চার ভাগ করেন, তাহলে বর্গক্ষেত্র পাবেন না, পাবেন সমকোণী চতুর্ভুজ, যাদের সম্মিলিত ক্ষেত্রফল (সেটা আপনি অনায়াসে বের করে নিতে পারবেন) দাঁড়াবে ২৪ বর্গসেন্টিমিটার—আরেকটু কাছিয়ে আসা হলো। ছবিটা একটু পরিষ্কার হচ্ছে, আশা করি। যত বেশিসংখ্যক খণ্ড বিন্দু নেবেন, ক আর খ- এর মাঝে ততই ৩২ বর্গমিটারের কাছে যেতে পারবেন ফলশ্রুত চতুর্ভুজগুলোর সম্মিলিত ক্ষেত্রফল যোগ করে। রেখাটিকে কত মিহি করে ভাগ করতে পারবেন আপনি? যত সূক্ষ্ম ইচ্ছে আপনার, একেবারে শূন্য না হলেই হয়। এই খণ্ডগুলো সব সমান মাপের হতে হবে তার কোনো প্রয়োজন নেই, তবে সমান হলে গুনতে সুবিধা, এই যা। তাছাড়া সমান-অসমান দুটিতে একই ফল পাওয়া যায় সচরাচর।

ভূমি-রেখার এই ছোট ছোট টুকরোগুলো অঙ্কের বইতে সাধারণত Δx সাংকেতিক চিহ্ন দিয়ে লেখা হয়। এই Δx দৈর্ঘ্যবিশিষ্ট রেখাখণ্ডের বাম বা ডান প্রান্তের বিন্দুর দূরত্ব যদি হয় x, আর সেখানকার লম্বরেখাটির উচ্চতা হয় ƒ(x), তাহলে সেই সরু চতুর্ভুজটির ক্ষেত্রফল হবে ƒ(x)Δx. সুতরাং এরকম সব ক্ষেত্রফল যোগ করলে একটি সংখ্যা দাঁড়াবে যাকে আমরা ∑ƒxΔ(x) ধরণের সাংকেতিক ভাষায় লিখতে পারি। ( ∑ দিয়ে s u m অর্থাৎ যোগফল বোঝাচ্ছে) এই Δx সংখ্যাটি শূন্য না হয়ে শূন্যের একেবারে গায়ে গায়ে ঘেঁষে যাওয়ার অবস্থায় দাঁড়ালেও যদি এই যোগফল কোনো সুনির্দিষ্ট সংখ্যাতে গিয়ে পৌঁছায় তাহলে সেই সংখ্যাটিকেই গণিতের সংজ্ঞায় বলা হয় ইন্টিগ্রাল (এক্ষেত্রে ত্রিভুজের ক্ষেত্রফল)। তার অর্থ দাঁড়াচ্ছে যে ক্ষেত্রফলও একটি লিমিটঃ

lim_∇r→0 Σf(x)Δx = ক্ষেত্রফল (১৪)

সজাগ পাঠক প্রশ্ন তুলতে পারেন, এবং অত্যন্ত যুক্তিযুক্তভাবেই, যে সামান্য একটা ত্রিভুজের ক্ষেত্রফল বের করতে অনর্থক এত পরিশ্রম করার কী দরকার ছিল, যেখানে ইউক্লিডের জ্যামিতি বইতেই তার জবাব দেওয়া আছে পরিষ্কার অক্ষরে? আমাদের উত্তর: ঠিক সেই কারণেই উদাহরণটি বাছাই করা, সবাই পরিচিত এর সঙ্গে। পরিচিত জিনিস দিয়ে একটা অপরিচিত আইডিয়া ব্যাখ্যা করা অনেক সহজ, আমাদের মতে।

এটা সত্য যে ত্রিভুজের বেলায় কাটাকুটি, আন্দাজ-অনুমান এসবের কোনোকিছুরই প্রয়োজন ছিল না, কিন্তু এর চেয়ে জটিলতর এলাকার ক্ষেত্রফল বের করতে হলে ইউক্লিড সাহেবের সাহায্যের জন্য হাত বাড়ালে লাভ হবে না, সেখানে এই কাটাকুটি, আন্দাজ-অনুমানই বলতে গেলে একমাত্র ভরসা। যেমন ধরুন একটা বৃত্তাকার মাদুরের ক্ষেত্রফল বের করতে বলছেন আপনার স্ত্রী। কিংবা একটা বড়সড় কলাপাতার ক্ষেত্রফল বের করতে বললেন কেউ। সেক্ষেত্রে ছোট ছোট চতুর্ভুজ বা ত্রিভুজ আকারের টুকরায় ভাগ করে শেষে লিমিটে চলে যাওয়া ছাড়া আর কী উপায় আছে আমি জানি না।

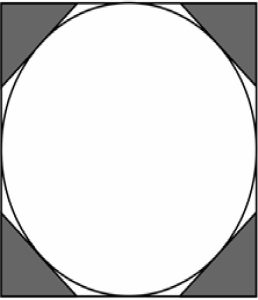
লিমিট নামের আইডিয়াটি বলতে গেলে বেশ আধুনিক, সপ্তদশ শতাব্দীতে ধীরে ধীরে অঙ্কুরিত হয়ে ঊনবিংশ শতাব্দীতে এসে পূর্ণ অবয়বে বিকশিত হয়ে ওঠে। কিন্তু অনেকগুলো ছোট চতুর্ভুজ যোগ করে বৃত্তজাতীয় কোনো জটিল এলাকার আনুমানিক ক্ষেত্রফল বের করার চেষ্টা আজকের নয়, অনাদিকাল থেকে চলে আসছে। খ্রি.পূ. সপ্তম শতকে জন্মলব্ধ মিসরীয় গাণিতিক আহমেস বৃত্তের ক্ষেত্রফল বের করার চেষ্টা করেছিলেন দারুণ বুদ্ধিমত্তা ও অন্তর্দৃষ্টির পরিচয় দিয়ে। প্রথমে একটি ৯ একক ব্যাসবিশিষ্ট বৃত্ত নিয়ে সেটাকে আটকালেন ঠিক ৯ একক লম্বা বর্গক্ষেত্রের ভেতর। খুব মোটা অনুমান হিসেবে এই বর্গের এলাকা আর বৃত্তের এলাকায় তেমন তফাত নেই। তবে এতে তিনি সন্তুষ্ট থাকলেন না। বর্গের চার কোনাতে চারটে স্পর্শক টেনে তৈরি করলেন চারটে সমদ্বিবাহু ত্রিভুজ। এই চারটে ত্রিভুজের ক্ষেত্রফল বের করা এমন কোনো শক্ত ব্যাপার নয়। সেই সম্মিলিত ক্ষেত্রফলকে তিনি বিয়োগ করে ফেললেন পুরো বর্গের ক্ষেত্রফল থেকে। এভাবে একটা সিদ্ধান্তে পৌঁছালেন তিনি যে ৯ একক ব্যাসবিশিষ্ট বৃত্তের ক্ষেত্রফল আর একটি ৮ একক ক্ষেত্রফল সমান।

সেটা অবশ্য ঠিক নয়, কিন্তু এতে গণিতের একটি সর্বজনীন অমূলদ সংখ্যা, π (পাই), যার আবিষ্কারের পেছনে সবচেয়ে বেশি প্রেরণা ছিল বৃত্তের, এবং যার আনুমানিক মান হিসেবে ধরা হয় ২২/৭ সংখ্যাটিকে, আহমেসের গণনাতে সেটা বেরিয়ে এল ১৯/৬-তে। অর্থাৎ তাঁরটি হলো ৩+১/৬, আর আসলটি ৩+১/৭। আশ্চর্য মিল, যখন চিন্তা করি দুয়ের মাঝে প্রায় ৪০০০ বছরের ফারাক। সেকালে মানুষ কীই বা জানতেন, তবু তাঁদের উপজ্ঞা (intuition) ছিল প্রখর, ‘আন্দাজ’ ছিল অসাধারণ। ঐতিহাসিকদের বিশ্বাস সে সময়কার মিসরীয় পণ্ডিতেরা পিরামিডের আয়তন বের করেছিলেন অঙ্ক কষে, যদিও তাঁদের ‘প্রমাণ’ কতখানি নির্ভরযোগ্য সেটা বিতর্কের বিষয়। সঠিক ফর্মুলাটি হলোঃ

পিরামিডের আয়তন = ১/৩ (উচ্চতা x ভূমির ক্ষেত্রফল)।

এতে কোনো সন্দেহ নেই যে মিসরীয়দের জানা ছিল এটি, সে যেভাবেই হোক। অ্যারিস্টটলের মতে এর নির্ভুল প্রমাণ দিয়েছিলেন গ্রিক গাণিতিক ডেমোক্রিটাস( জ. ৪৬০ খ্রি.পূ., আ.), যদিও সে দাবিটাও প্রমাণসাপেক্ষ।

আধুনিক লেখকদের মতে, হয়তো একটা প্রমাণ তিনি দিয়েছিলেন, কিন্তু সম্ভবত বর্তমান যুগের উন্নতমানের যুক্তির বিচারে ধোপে টেকার মতো ছিল না। ভারতবর্ষের আর্যভট্ট নিজেও একটা সূত্র দিয়েছিলেন পিরামিডের ঘনফলের জন্য, কিন্তু তাঁর ফর্মুলাতে ৩-এর জায়গায় ছিল ২ (হয়তো ত্রিভুজের উদাহরণ দ্বারা প্রভাবিত হওয়ার কারণেই)। গাণিতিকভাবে বিশুদ্ধ ও গ্রহণযোগ্য প্রমাণ, সেটা পিরামিডের ঘনফলই হোক আর বৃত্তের ক্ষেত্রফলই হোক, তাতে ক্যালকুলাসের সমকক্ষ আর কিছু নেই। অন্তত এখনো পর্যন্ত।

খেয়াল করুন যে আমরা এখনো ক্যালকুলাসের দ্বিতীয় শাখাটি নিয়ে টু শব্দ করিনি—অন্তরকলন ক্যালকুলাস (Differential Calculus)। স্কুল কলেজের পাঠ্যসূচিতে প্রথমে শেখানো হয় অন্তরকলন, তারপর সমাকলন। আমরা ঠিক উলটো পথটা বাছাই করলাম এখানে, কারণ মৌলিক যুক্তিতর্কের দিক থেকে অন্তরকলনই হল বেশি জটিল। এতে, পর্দার আড়ালে, আছে সেই 0/0 এর ব্যাপারটি, যদিও কলেজের প্রথম বর্ষের ছাত্রছাত্রীরা দু-তিন ক্লাস করার আগে টেরই পায় না সেই জটিলতাটুকুর উৎস কোথায়, বা আদৌ কোনো জটিলতা আছে কি না। যান্ত্রিক দক্ষতার সাথে অঙ্ক কষে ভালো নম্বর পাওয়া এক জিনিস, আর তার মর্মমূলে গিয়ে সারবস্তুটুকু উদ্ধার করতে পারা অন্য জিনিস। একটু আগেই তো বললাম, লিমিট বড় রহস্যময় জিনিস। প্রথম বছর তারা শেখে, দ্বিতীয় বছর মুখস্থ করে, যাতে কাজ চালানোর দক্ষতা আসে, তৃতীয় বছর তারা ভাবে, এত দিনে ব্যাপারটা সত্যি সত্যি বোঝা গেল। কতগুলো জিনিস আছে সংসারে যেগুলো বুঝতে একটু সময় লাগে। শুধু বই-পুস্তক আর শিক্ষক-অধ্যাপকই যথেষ্ট নয়। তার জন্য লাগে মানসিক ও বৌদ্ধিক পরিপক্বতা, একটু সৃজনশীলতাও। হ্যাঁ, এটা আমার (মী.র) ব্যক্তিগত অভিমত যে কোনো সৃজনশীল মানুষের কাজ ভালো করে বুঝতে হলে নিজেরও খানিক সৃজনশীলতা থাকা দরকার। সেটা শিল্পকলাই বলুন আর গণিত বিজ্ঞানই বলুন। স্রষ্টার মস্তিষ্কের ভেতরে প্রবেশ করার আগে কি কেউ পুরোপুরি বুঝতে পারে কারো কাজ ?

অন্তরকলন বোঝাতেও সেই একই ত্রিভুজের উদাহরণ ব্যবহার করব। সহজ, চোখে দেখা যায়, অথচ এতেই একটা মোটামুটি ধারণা দাঁড় করানো সম্ভব। এবার আমরা ত্রিভুজের ক্ষেত্রফল নিয়ে আগ্রহ প্রকাশ করব না। আমরা কল্পনা করব যে সমকোণী ত্রিভুজটির অতিভুজ একটা পাহাড়ি জায়গার খাড়া রাস্তা। ক থেকে গ পর্যন্ত পাহাড়ের গা বেয়ে উঠতে হলে আমাদের জানা দরকার কতখানি চড়াই, অর্থাৎ তার ঢাল (slope) কত। কিভাবে বের করব সেটা? সোজা! লম্ব খ-গ রেখাটির দৈর্ঘ্যকে ভাগ করুণ ভূমিস্থ ক-খ রেখাটির দৈর্ঘ্য দিয়ে। একেই আমরা বলি ‘ঢাল’। খেয়াল করুন যে ‘ঢাল’ যদি শূন্য হয় (যার অর্থ গ আর খ একসাথে মিশে যাওয়া), তাহলে একেবারে সমতল, অর্থাৎ কোনো রকম চড়াই-উতরাই নেই। আবার যদি অসীম হয় তাহলে কী হবে? তার অর্থ খাড়া পাহাড়, একেবারে লম্বালম্বি উঠে গেছে। ‘অসীম’ কিন্তু এসে গেল এখানে। কেন হলো এরকম? হলো এজন্য যে পর্বত খাড়া হওয়া মানে খ বিন্দুটি ক-এর নিকটে আসতে আসতে একেবারে মিশে যাবার উপক্রম হচ্ছে, আর ওদিকে খ-গ রেখাটির দৈর্ঘ্য মোটেই বদলাচ্ছে না। তার অর্থ একটা সসীম সংখ্যাকে একটা অত্যন্ত ক্ষুদ্র সংখ্যা দিয়ে ভাগ করা হচ্ছে। সেই কারণেই ভগ্নাংশটি অসীমের পানে ছুটে যাচ্ছে সোল্লাসে।

যেহেতু ত্রিভুজটি গোড়া থেকেই ছিল সমদ্বিবাহু ও সমকোণী, আমরা জানি যে লম্ব/দৈর্ঘ্য=১, কারণ ক-খ আর খ-গ দুটি রেখারই সমান দৈর্ঘ্য। এবার কল্পনাতে আপনি খ-গ রেখাটির সমান্তরালতা বজায় রেখে তাকে সরিয়ে আনুন কেন্দ্রের পাশে, অর্থাৎ ক-এর কাছে। দুটি দৈর্ঘ্যই সংকুচিত হয়ে যাচ্ছে, কিন্তু তাদের অনুপাত থাকছে একই। কাছে বলতে কিন্তু কাছেই বোঝানো হচ্ছে, মানে যত কাছে আসা সম্ভব, যতক্ষণ না অবশ্য হুমড়ি খেয়ে পড়ে যায় ক-এর ঘাড়ের ওপর। ক্ষুদ্র ত্রিভুজটি বড়টির সদৃশ হলেই হলো, অর্থাৎ বাহুগুলোর অনুপাতে যেন কোনো রদবদল না হয়। এবার মাপ নিয়ে দেখুন দুটি বাহুর দৈর্ঘ্য, এত ছোট হয়ে গেছে যে রুলার বসানোরও উপায় নেই বলতে গেলে। ধরা যাক, ভূমিটুকুর দৈর্ঘ্য Δx আর লম্বের দৈর্ঘ্য Δy .সুতরাং অতিভুজটির ঢাল দাঁড়াচ্ছে Δy/Δx, যা আমরা একটু আগেই দেখলাম। এবং যার মান আগের মতোই অপরিবর্তিত— ১

তাহলে কি আমরা লিখতে পারি না

lim_Δx→0 Δy/Δx=? (১৫)

অবশ্যই পারি।

আশা করি আইডিয়াটির একটা ভাসা ভাসা ধারণা পাওয়া গেল। একটা ভগ্নাংশের লব আর বিভাজক যদি একেবারে শূন্য হয়ে যায়, তাহলে সে অস্তিত্ব হারিয়ে ফেলে, তার কোনো মানে থাকে না। কিন্তু যদি দুটোই সমান হারে ছোট হয়, তুচ্ছাতিতুচ্ছ শূন্যতায় পৌঁছায়, তাহলে তাদের যে অনুপাত, সেটির একটা ‘লিমিট’ থাকলে থাকতেও পারে, এবং সেই লিমিটের একটা জ্যামিতিক তাৎপর্য আছে বৈকি—এক ক্ষেত্রে সেটা হতে পারে কোনো রেখাবেষ্টিত সমতল ক্ষেত্র, আরেক ক্ষেত্রে হয়তো বা রেখার ঢাল।

ওপরের উদাহরণটি একটা ছেলেমানুষি উদাহরণ, মানছি, ছোট বাচ্চাও বুঝবে অনায়াসে। এবং সেই কারণেই নেওয়া। আমাদের বক্তব্য হল যে ত্রিভুজ আর সরলরেখা না হয়ে যদি বৃত্ত, পরিবৃত্ত, অধিবৃত্ত কিংবা তার চেয়েও জটিল কোনো রেখা হতো, তাহলেও প্রায় একই যুক্তি চালানো যেত। ঢালের সংজ্ঞাতে যা করা হয় সাধারণত, সেটা হলো দুটি কাছাকাছি বিন্দু নেওয়া রেখাটির ওপর। এবং প্রথমে বিন্দু দুটিকে একটি সরলরেখাতে যুক্ত করে তার ঢাল মাপা, ওপরে যে পদ্ধতিটা ব্যবহার করা হলো, ঠিক সেই পদ্ধতিতে। তারপর সেই বিন্দুদ্বয়কে পরস্পরের কাছে টেনে নেওয়া; কাছে, আরো কাছে, যত কাছে আপনার কল্পনায় সম্ভব। সবশেষে সেই ঢালটির ‘লিমিট’ নেওয়া, ঠিক আগেরই মতো করে। রেখাটি যদি যথেষ্ট ‘সুশীল’ হয়, অর্থাৎ হঠাৎ খাড়া হয়ে না যায়, বা বলা নেই কওয়া নেই, অকস্মাৎ বেঁকে না যায়, অথবা রেখাটি সেই বিন্দুতে গিয়ে একেবারে উধাও হয়ে না যায়, তাহলে সেই লিমিটটিও সাধারণত ভদ্র ব্যবহার করবে, অর্থাৎ তার একটা সসীম মান থাকবে।

এই সহজ আইডিয়াগুলো আজকের মনমানসিকতায় একেবারে ডালভাত মনে হতে পারে, কিন্তু সপ্তদশ শতাব্দীর উষালগ্নে সেগুলো মোটেই সেরকম ছিল না। বরং লোকে হাসাহাসি করত যখন কেউ উল্লেখ করত। শূন্য অথচ শূন্য নয়, ‘ক্ষুদ্রাতিক্ষুদ্র’ তবে একেবারে শূন্য নয়, এসব তো স্রেফ হেঁয়ালি বলে অভিযোগ করত অনেকে। আইজ্যাক নিউটন নিজেও, infinitesimal শব্দটা মনেমনেই ভেবেছিলেন, প্রকাশ্যে উচ্চারণ করতে সাহস পাননি, পাছে না কেউ পাগল ভেবে বসে তাঁকে। সেজন্য তাঁকে ঘুরিয়ে-ফিরিয়ে বলতে হয়েছে একই কথা—নানা রকম উদ্ভট শব্দ প্রয়োগ করে। যেমন ‘ফ্লাক্সিয়ন’।

আইজ্যাক নিউটন মানবেতিহাসের সেরা প্রতিভাদের একজন ছিলেন তাতে কারোই কোনো সন্দেহ নেই; এত বড় মাপের মানুষ হাজার বছরে দু-চারজনই জন্মায়। ভিঞ্চি ছিলেন সেই ক্ষণজন্মা পুরুষদের একজন। তারপর গ্যালিলি। তারপরই আমি (মী.র) স্থান দিই এই লোকটিকে। সাধারণ মানুষদের কল্পনাতে নিউটন আর আইনস্টাইন যেন দুটি কিংবদন্তীয় যুবরাজ, সর্বগুণে গুণবান, সর্বরূপে রূপবান, সর্বমেধায় মেধাবী। সর্বকালের সর্বশ্রেষ্ঠ চিত্রতারকাদের মতো। কিন্তু তাঁদের ব্যক্তিগত জীবনের খবর অনেকেরই জানা নেই, এবং এক হিসেবে জানার দরকারও নেই। মহৎ সৃষ্টির স্মৃতিই হোক মহৎ স্রষ্টার জীবনকাহিনি, এটা আমি সব সময়ই বলে থাকি। তাঁদের ব্যক্তিগত জীবন নিয়ে না-ই বা করলাম অহেতুক ঘাঁটাঘাঁটি। তবু কথা থাকে, বিশাল প্রতিভাই জাগায় বিপুল কৌতূহল। লোকটা কে? তিনি কি আমাদের মতোই রক্তমাংসে গড়া মানুষ? আমাদের মতোই ভাত-কাপড় আর সংসারধর্ম নিয়ে ব্যতিব্যস্ত থাকেন তাঁরা? হয়তো ঠিক তা নয়। তবে তাঁদের জীবনও অনেক সময় চিত্রতারকাদের মতোই বিচিত্র মনে হয়। তাঁরা আমাদের মতো রক্তমাংস আর সুখদুঃখ, রোগশোকে গড়া মানুষ হয়েও আমাদের চেয়ে আলাদা।

নিউটনের কথাই ধরুন। কথিত আছে যে তিনি জন্মের প্রথম মুহূর্ত থেকেই পৃথিবীর আর সব নবজাতকদের থেকে আলাদা ছিলেন। ১৬৪২ সালের ২৫ ডিসেম্বর তাঁর জন্মদিন। অপূর্ণকালিক জন্ম। এত ছোট আকারের শিশু গোটা ব্রিটেনে সম্ভবত জন্মায়নি তার আগে-দু-চার পাউন্ডের বেশি ওজন ছিল না তাঁর। গ্রামের লোকেরা বলত, নিউটনকে একটা মদের গ্লাসের ভেতর পুরে রাখা যাবে অনায়াসে। তাঁর কৃষিজীবী বাবা-মা কারোরই কোনো আশা ছিল না ছেলে বাঁচবে। কিন্তু ছেলে যে বেঁচে ছিল সেটা পৃথিবীসুদ্ধ লোক জানে আজকে। দুর্ভাগ্যবশত নিউটনের বাবা ছেলের কীর্তিকাহিনি কিছুই দেখে যেতে পারেননি; মাত্র ছত্রিশ বছর বয়সে তিনি ইহলোক ত্যাগ করে চলে গেলেন যুবতী স্ত্রীর ওপর বৈধব্যের ভার গছিয়ে, নিউটনের জন্মেরও দুমাস আগে। দু-তিন বছর পর অবশ্য বিধবা আবার বিয়ে করেন স্থানীয় চার্চের পাদ্রিকে, যেটা বোধ হয় শিশু নিউটন খুব একটা পছন্দ করেননি। ছেলে চলে যায় নানার বাড়িতে। মনে মনে এমনই রাগ ছেলের যে কয়েক বছর পর যখন মা তাঁর ছেলেকে ডেকে পাঠান, তখন মায়ের ডাকে সাড়া দেওয়া দূরে থাক, তিনি নাকি এমন হুমকি দিয়েছিলেন যে গ্রামে গেলে মায়ের ঘরে আগুন লাগিয়ে দেবেন। পরে অবশ্য মা-ছেলেতে মিটমাট হয়ে গিয়েছিল সব। এমনকি পরিণত বয়সে নিউটন দারুণ মাতৃভক্ত হয়ে পড়েছিলেন, নিউটনের জীবনীকারদের অনেকেই সেটা উল্লেখ করেছেন।

নিউটনের মা কোনো দিন ভাবেননি ছেলেকে স্কুলে পাঠাবেন; কৃষকের ছেলে কৃষিকর্ম করবে, খেতখামার, গরু-ছাগল দেখবে, বাপ-দাদা চৌদ্দপুরুষ যা করে এসেছে, এই ছিল তাঁর মনোবাসনা। কিন্তু ছেলের যে চাষবাসের দিকে বিন্দুমাত্র মনোযোগ নেই, অবসর সময়টা বরং গ্রামের লাইব্রেরিতে কাটাতেই বেশি আগ্রহ, সেটা তিনি জেনেও না জানার ভাব করে থাকতেন। বড় হলে সব ঠিক হয়ে যাবে——যেমন করে ভাবেন সব দেশেরই বাবা-মায়েরা। সৌভাগ্যবশত নিউটনের এক কাকা ছিলেন চার্চের পাদ্রি। তিনি ভ্রাতুষ্পুত্রের মেধার গন্ধ পেয়েছিলেন। বুঝতে পেরেছিলেন যে এ ছেলে হালচাষ করে সুখী হবার নয়। তিনিই মাকে বুঝালেন যে নিউটনকে স্কুলে যেতে না দেওয়া অন্যায় হবে। মা মেনে নিলেন তাঁর যুক্তি কত ভাগ্য আমাদের! তার পরই তাঁর লেখাপড়ার জীবন শুরু। কিন্তু স্কুলে যাওয়ার সঙ্গে সঙ্গে কি নিউটনের বিশাল মেধার পরিচয় প্রভাতের রবিকরের মতো উদ্ভাসিত হয়ে উঠেছিল? মোটেও না। তাঁর চেয়েও ভালো রেজাল্ট করা ছেলে আরো দু-চারজন ছিল একই ক্লাসে। বন্ধুবান্ধবও ছিল না বেশি। একা একা থাকতেই যেন বেশি পছন্দ করতেন। লাজুক, আড়ালপ্রিয়, লোকভয়, এর সবই ছিল তাঁর চরিত্রে, ছোটবেলায় শুধু নয়, পরিণত বয়সে যখন তিনি ইউরোপব্যাপী গৌরবের চরম শিখরে আরূঢ়, তখনো। তাঁর স্কুলজীবনের সেই ছাড়া ছাড়া ভাব, সেই আপাত- বৈরাগ্য, অন্য কারো সাথে মেলামেশা না করার প্রবণতা, তাঁকে সহজেই নানা রকম হাসিঠাট্টা, ব্যঙ্গবিদ্রূপের শিকার করে তুলেছিল। একবার স্কুল-প্রাঙ্গণে এক ছেলের সঙ্গে বেশ বড়-রকমের ঝগড়া বেঁধে যায় তাঁর; ছেলেটি ছিল সেবছরের সেরা ছাত্র। সবার সামনে ভীষণভাবে অপমান করে তাঁকে, মারধরও করে থাকতে পারে। স্কুলবয়সে ছেলেমেয়েদের কতই বা হিতাহিতজ্ঞান। মজার ব্যাপার যে সেই প্রকাশ্য অপমান আর লাঞ্ছনাই বোধ হয় নিউটনের ভেতরকার সুপ্ত বজ্রকে জাগিয়ে তুলতে সক্ষম হয়েছিল। স্কুলের বাঁদর ছেলেমেয়েদের উৎপীড়নে অস্থির হয়ে বাচ্চারা যেমন রাগে-দুঃখে পণ করে মনে মনে যে একদিন তাকে দেখিয়ে দেবে সত্যিকার জোর কার গায়ে, তেমনি কোনো পণ করেছিলেন কি না নিউটন নিজে সঙ্গে জানি না, কিন্তু সেই ঘটনার পর থেকে সেই যে পড়াশোনার জগতে ঢুকলেন তিনি, বলতে গেলে, সেখানেই আত্মবন্দী হয়ে থাকলেন সারা জীবন। সেই বছরই তিনি সেই উৎপীড়ক ছেলেটিকে হার মানিয়ে অনেক অনেক ওপরে চলে গেলেন, যেখানে আরোহণ করার সাধ্য ছিল না কারো। পাঠ্যবিষয়ের সবকিছুতেই সমান পারদর্শিতা অর্জন করেছিলেন নিউটন তেমন দাবি করা যাবে না, কিন্তু গণিত আর পদার্থবিজ্ঞান (সে যুগে যাকে natural philosophy বলা হতো ব্রিটেনে, সম্ভবত ইউরোপের গ্রিক-প্রভাবিত সাংস্কৃতিক ঐতিহ্যেরই কারণে), এই দুটি বিষয়ে নিউটনের দখল সারা মহাদেশে আর কারো ছিল কি না সন্দেহ, সেই স্কুলবয়সেই।

যা-ই হোক, স্কুল পাস করলেন তিনি কৃতিত্বের সাথেই, যদিও গণিত আর বিজ্ঞান ছাড়া অন্যান্য বিষয়ে তাঁর স্বভাবজাত ঔদাসীন্যের কারণে সর্বমুখী সাফল্যের পরিচয় দেওয়া সম্ভব হয়নি। স্কুল পাসের পর তিনি গেলেন কেম্ব্রিজ বিশ্ববিদ্যালয়ের বিখ্যাত কলেজ ট্রিনিটিতে ভর্তি হতে, ১৬৬০ সালে, যখন তাঁর বয়স আঠারো। ভর্তি তিনি অনায়াসেই হয়ে গেলেন, কিন্তু সেই লাজুক স্বভাব আর লোকচক্ষুর বাইরে থাকার আজন্ম প্রবণতা, দুয়ে মিলে কেম্ব্রিজেও কারো চোখে পড়ার মতো দারুণ কিছু করে ফেলেননি। তার ওপর নিউটনের ছিল আর্থিক সমস্যা। মাসিক খরচ চালানোর জন্য সেই ছাত্রাবস্থাতেই টুকিটাকি কাজ করতেন তিনি কলেজের কিচেন বা অধ্যাপক পাড়ায়। স্কুলের মতো কেম্ব্রিজেও নিউটন ছিলেন আর দশটা ছাত্রের মতোই-অলক্ষণীয় ও অবিশিষ্ট। তবে নিজের ঘরের নিরালাতে বসে তিনি জ্ঞানসাধনা করেননি তা নয়। বলা হয় যে স্নাতক ছাত্র থাকাকালেই বেশ কিছু মৌলিক চিন্তা তাঁর মাথায় আসে যা তিনি কারো কাছে প্রকাশ করেননি বা কারো সঙ্গে আলাপ-আলোচনা করেননি সেসব বিষয়ে। এই আরেকটা অদ্ভুত স্বভাব ছিল লোকটার-ভীষণ গোপন-প্রিয়তা। সব সময় যেন একটা আতঙ্কে থাকতেন পাছে না কেউ তাঁর আইডিয়া চুরি করে নেয়। একটা অসুস্থ সন্দেহপরায়ণতা, এমন অননুকূল উক্তিও করেছেন বেশ কিছু জীবনীকার।

১৬৬৫ সালে বিএ পাস করলেন বেশ কৃতিত্বের সঙ্গেই, যদিও তাঁর মতো অসামান্য মেধাবী ছাত্রের কাছ থেকে যতটা সাফল্য আশা করা যেত সেটুকু সাফল্য হয়তো অর্জন করা হয়নি। সম্ভবত একই কারণে, গণিত আর বিজ্ঞান-বহির্ভূত বিষয়ের প্রতি নিদারুণ অনাগ্রহ। কিন্তু গণিতে তিনি ছিলেন ক্লাসের উজ্জ্বলতম তারকা। অসম্ভব ভাল রেজাল্ট করেছিলেন গণিতে, কিন্তু সেখানেও সারা বিশ্ববিদ্যালয়জুড়ে যে নাম করে ফেলা, সবার চোখে তাক লাগিয়ে দেওয়া, সেটা হয়ে ওঠেনি, প্রধানত সেই লোকচক্ষুর-দূরে-থাকা স্বভাবেরই জন্য। গোটা গণিত বিভাগের কেবল একটি গুণী লোকেরই দৃষ্টি আকর্ষণ করতে সক্ষম হয়েছিলেন তিনি—কেম্ব্রিজের সে সময়কার লুকাসিয়ান প্রফেসর আইজ্যাক ব্যারো। তিনিই ছিলেন একমাত্র শিক্ষক নিউটনের যিনি তাঁর ছাত্রটির ভেতরের আগুন দেখতে পেরেছিলেন। বুঝতে পেরেছিলেন এ ছেলে বড় কিছু করবে ভবিষ্যতে। যেটা তিনি জানতেন না তা হলো সেই ভবিষ্যৎ তখনই সমুপস্থিত দুয়ারে। পৃথিবী এখনই কেঁপে উঠবার উপক্রম। অনাগত ভবিষ্যৎ স্বাগতের অপেক্ষায় আঙিনায় দাঁড়িয়ে।

১৬৬৫ সালের গ্রীষ্মকালে সারা দেশব্যাপী এক মারাত্মক ব্যাধির প্রাদুর্ভাব হয়। এমন সর্বনাশা সেই মহামারি যে গোটা বিশ্ববিদ্যালয়ই বন্ধ হয়ে যায় অনির্দিষ্টকালের জন্য। সে বন্ধ বন্ধই থাকল পুরো দুবছর। নিউটন কলেজ ছুটির পরমুহূর্তেই চলে গেলেন গ্রামের বাড়িতে। শুধু গেলেনই না, বলতে গেলে, দরজা বন্ধ করে ধ্যানমগ্ন সাধুসন্ন্যাসীর মতো জ্ঞানসাধনার একনিষ্ঠ ব্রততে আত্মনিমগ্ন হয়ে থাকলেন। খাওয়া-পরা-ঘুম-আরাম সব বাদ দিয়ে এক আবিষ্ট আত্মার মতো বইখাতা আর অঙ্কের মধ্যে ডুবে রইলেন। বিপুল এই পৃথিবীর কোথায় কী হচ্ছে, কোথায় কী ওলটপালট হচ্ছে, কে কোন রহস্যপুরীর সন্ধান নিয়ে এল জড়জগতের মরমানবের জন্য, তার কোনোকিছুতেই তাঁর ছিল না বিন্দুমাত্র আগ্রহ। প্রথম যৌবনের পরিচিত আবেগ আর উচ্ছ্বাস নিউটনের জীবন থেকে ছিল সম্পূর্ণ নির্বাসিত। ওসবের কোনো অনুভূতিই যেন ছিল না তাঁর। ইউরোপের প্রখ্যাত গাণিতিক ও আইনজ্ঞ মারকুই লোপিতাল নিউটনকে দেখতেন একরকম জ্যোতিষ্কের মত, যেন এ জগতের কেউ ছিলেন না তিনি। লোপিতালের বিখ্যাত উক্তি” ‘আমার মানসপটে আমি তাঁকে দেখি দূরনীহারিকাবাসী এক নভোচারী প্রতিভা হিসেবে’। পরবর্তীকালের বিশ্ববিখ্যাত ব্রিটিশ কবি ওয়ার্ডসওয়ার্থ ট্রিনিটি কলেজ প্রাঙ্গণে নিউটনের প্রস্তরমূর্তি দেখে অনুপ্রাণিত হয়ে লিখেছিলেনঃ

‘…Newton, with his prism and silent face

The marble index of a mind

Voyaging through the strange seas of thought alone’.

আসলেও তাই। নিউটনের জীবনী পড়লে অবাক বিস্ময়ে বিহ্বল হয়ে থাকা ছাড়া উপায় থাকে না সাধারণ মানুষের।

এবার বলি গ্রামের বাড়িতে সেই দুটি অপ্রত্যাশিত ছুটির বছর তিনি কিভাবে কাটিয়েছিলেন। ১৬৬৫-এর আগস্ট থেকে ১৬৬৭-এর আগস্ট—এই দুটি বছরই ছিল তাঁর জীবনের সবচেয়ে গৌরবময়, সবচেয়ে দিব্যজ্যোতিপূর্ণ, সৃজনোল্লাসমুখর সময়কাল। বলা হয় যে ওই দুটি বছরের মধ্যে যুবক নিউটন যা আবিষ্কার করেছিলেন তার সমতুল্য কাজ তাঁর ৮৪ বছরের দীর্ঘ আয়ুষ্কালে আর কখনো করা হয়নি, এবং সে কাজের সঙ্গে তুলনা হতে পারে এমন বিরল প্রতিভাধর মানুষ তাঁর

মূল উক্তি – ‘I picture him to myself as a celestial genius’.

আগে বা পরে জন্মগ্রহণ করেননি, অন্তত বিজ্ঞান-গণিতের ক্ষেত্রে। বর্ণনাটি নিউটনের নিজের ভাষাতেই দেওয়া ভালো”:

১৬৬৫-এর গোড়াতে আমি দুটি জিনিস আবিষ্কার করলাম। এক: সংখ্যার রাশিমালার যোগফল বের করার পদ্ধতি; দুই: দ্বিসংখ্যাবিশিষ্ট ঘাতকে (power) কিভাবে যোগরাশিতে প্রকাশ করতে হয় (binomial theorem বা দ্বিঘাতী সূত্র)। একই বছর মে-তে (সম্ভবত কেম্ব্রিজে থাকাকালেই) আমি পেলাম গ্রেগরি আর ফ্লসিয়াসের স্পর্শক পদ্ধতি। নভেম্বরে পেলাম ফ্লাক্সিয়নের সরাসরি তত্ত্ব (অন্তরকলন ক্যালকুলাস)। পরবর্তী জানুয়ারিতে আবিষ্কার করলাম বর্ণতত্ত্ব। সেই মে-তেই পেয়ে গেলাম অন্তরকলনের বিপরীতটি, সমাকলন। একই বছর চিন্তাভাবনা করতে লাগলাম মাধ্যাকর্ষণ শক্তি বিষয়টি নিয়ে, যে শক্তি চাঁদের অক্ষ পর্যন্ত বিস্তৃত। নিজ অক্ষপথে চন্দ্রগ্রহণের নিয়মানুগ প্রদক্ষিণের জন্য বিশ্বপৃষ্ঠ হতে যে পরিমাণ আকর্ষণশক্তির প্রয়োজন তার মাপজোক করে একটা সন্তোষজনক সিদ্ধান্তে পৌঁছানো গেল। এ সবই আমি করতে পেরেছিলাম ১৬৬৫ থেকে ১৬৬৬, এই দুটি বছরের মধ্যে। ওটিই ছিল আমার উদ্ভাবনী জীবনের স্বর্ণযুগ। ওই সময়টুকুতে আমি যতটা মনোযোগ দিতে পেরেছি গণিত আর দর্শনের ওপর ততটা কখনোই দেওয়া হয়নি। মাত্র দুটি বছর! যৌবনে যা আমরা অলস দিবাস্বপ্নতেই কাটিয়ে দিই, যার কোনো মূল্যই দেওয়া হয়না সময় থাকতে, সেই দুটি অমর বছরই তিনি উপহার দিয়ে চিরধন্য করে করে গেছেন বিশ্ববাসী গোটা মানবজাতিকে, জাতি-ধর্ম-বর্ণ-

মূল উক্তি: ‘In the beginning of the year 1665, I found the method of approximating series and the rule for reducing any [power] of any binomial to such a series [i.e.,binomial theorem]. The same year in May [probably while still at Cambridge] I found the method of tangents of Gregory and Slusius, and in November had the direct method of fluxions [differential calculus] and the next year in January had the theory of colours and in the May following I had the entrance into the inverse method of fluxions [ integral calculus] and in the same year I began to think of gravity extending to the orb of the moon…. and having thereby compared the force requisite to keep the moon in her orb with the force of gravity at the surface of the earth, I found them to answer pretty nearly. All this was in the two years 1665 to 1666 for in those years I was in the prime of my age for invention and minded mathematics and philosophy more than anytime since.’
(Portsmouth Collection,Sec.I,div. X, number 41, quoted from the article ‘Newton on Particles and Kinetics’ in The world of the Atom, ed.Henry A. Boorse and Lloyd Motz, Basic Books, Inc., publishers, New York and London,1966).

গোত্রনির্বিশেষে। সেকথা নিউটন নিজেও হয়তো জানতেন না তখন। মানুষ কি কখনো জানতে পারে তার সৃষ্টির পূর্ণ তাৎপর্য বা মূল্য কতটুকু। কিন্তু আমরা জানি নিউটন আর সকল স্রষ্টার চেয়েও বড় স্রষ্টা ছিলেন।

অনেকে মনে করে, বিশেষ করে জ্ঞানসৃষ্টির যথার্থ প্রকৃতির সঙ্গে যারা পরিচিত নয়, যে আলবার্ট আইনস্টাইন নিউটনের বলবিদ্যাকে ‘ভুল’ প্রমাণিত করে গেছেন। যারা এ কথা বলেন, তাঁরা হয়তো বুঝবেন না যে নিউটনের বিজ্ঞান জানা না থাকলে আইনস্টাইনও হয়তো আইনস্টাইন হতে পারতেন না। জ্ঞানবিজ্ঞানের কোনো শাখারই কোনও নতুন আবিষ্কার হঠাৎ আকাশ থেকে ঝরে পড়ে না। সবকিছুরই একটা পরিক্রমা আছে, একটা যৌক্তিক ধারাবাহিকতা আছে। নিউটনের বিস্ময়কর সৃষ্টিশীলতার ওপর মন্তব্য করতে গিয়ে অনেক ভাষ্যকারই ভাষা হারিয়ে ফেলেছেন। অনেকে বলেছেন, নিউটন এমনই নাছোড়বান্দা হয়ে লেগে থাকতেন একটা জিনিস নিয়ে, এবং দিনের পর দিন, রাতের পর রাত না খেয়ে, না নেয়ে তা নিয়ে মনের ভেতর বারবার ঘুরপাক খাওয়াতেন যে শেষ পর্যন্ত প্রকৃতিদেবী স্বয়ং তাঁর কাছে নতি স্বীকার করে তার সমস্ত রহস্য উদোম করে দিতেন তাঁর কাছে। তিনি ছিলেন প্রকৃতির প্রিয়তম বরপুত্র, এধরনের মন্তব্যও করেছেন কেউ কেউ।

পাঠক হয়তো খেয়াল করে থাকবেন যে নিউটন তাঁর ‘দুটি বছরের’ বয়ান শোনাতে আরেকটি মস্ত বড় আবিষ্কারের কথা উল্লেখ করতে বেমালুম ভুলে গিয়েছিলেন, বা তিনি ওটাকে একেবারেই উল্লেখযোগ্য মনে করেননি। সেটা হলো পদার্থের গতিসম্পর্কীয় গতির চালিকাশক্তির উৎস কোথায়। কী সমীকরণ দ্বারা আবদ্ধ গতি আর শক্তি যাকে আমরা বই-পুস্তকে গতিসূত্র ( laws of motion ) বলে জানি, সেগুলোও সেই দুটিমাত্র বছরের মধ্যেই করা। সে যে কী সুদূরপ্রসারী কাজ তার মর্ম শুধু পদার্থবিদেরাই জানে না, প্রতিটি প্রকৌশলী, প্রতিটি বিজ্ঞানসাধককে জানতে হয়, বিশ্বব্যাপী শিক্ষাপ্রতিষ্ঠানের সকল ছাত্রছাত্রীকে জানতে হয়, মুখস্থ করতে হয়। মোটমাট তিনটি সূত্র তাতেঃ

(১) জাড্যনীতি (law of inertia), যেটা আসলে গ্যালিলির সূত্র বলেই ধরা হয় (আগের একটি অধ্যায়ে আমরা উল্লেখও করেছি সেটা), একটা জিনিস যদি অলসভাবে কোথাও ঠায় বসে থাকে তাহলে তাকে ‘ঠেলে’ নাড়ানো ছাড়া অন্য কোনোভাবে নাড়াতে পারবে না কেউ। অর্থাৎ তাকে ‘জোর’ করে সরাতে হবে। ঠায় বসা না থেকে যদি কেউ ধীরবেগে চলতে থাকে সরলরেখাতে তাহলে তার ‘ধীরতা’ বদলাবার জন্যও একটু ঠেলার প্রয়োজন। নিউটন এটিকে তাঁর সূত্রাবলির প্রথম সূত্রের সম্মান দিলেন।

(২) ভর× ত্বরণ=বল (mass x acceleration = force) ।

(৩) ক্রিয়া-প্রতিক্রিয়া একবারে সমান সমান ও বিপরীতমুখী (action and reaction are equal and opposite)|

এই তিনটি সূত্রতে মিলে বিশ্বভুবনে যা কিছু চলে বা একেবারে চলেই না, কিংবা চললেও ভীষণ ঢিমেতালে, যে শক্তি নিজেকে কোনো কিছুর ওপর আরোপ করে তাকে চালাতে চেষ্টা করে, তার সবকিছুর ওপরই নিরবচ্ছিন্ন রাজত্ব করে গেছে নিউটনের ত্রিসূত্রমালার এই আশ্চর্য আলোকবর্তিকাটি। অথচ এই অসামান্য রকম ‘সামান্য’ জিনিসটির কথা তাঁর মনেই ছিল না আত্মজীবনী লেখার সময়! এমনই বিস্ময়কর ছিল নিউটনের মেধাজগৎ।

তিনটি সূত্রের মধ্যে সবচেয়ে বেশি ব্যবহৃত হয় বোধ হয় দ্বিতীয়টি, যাকে সাধারণ ভাষায় গতির দ্বিতীয় সূত্র বলে আখ্যায়িত করা হয় (second law of motion)। তবে এ সূত্রটি ততটা শক্তি হয়তো পেত না যদি না তিনি এটিকে তাঁর নিজেরই সদ্য আবিষ্কৃত অন্তরকলনের ভাষায় প্রকাশ করতে পারতেন। এই ভাষাতে সূত্রটি দাঁড়ায়ঃ

F = mdv/dt (১৬)

এখানে F হলো বল বা force, m হলো ভর, আর । গতি বা velocity. নিউটনের সমসাময়িক যুগে কোনো বস্তুর ভর গতির সঙ্গে বদলায় না, এটাই ছিল সর্বস্বীকৃত বিশ্বাস। সে কারণে উপরোক্ত সূত্রটিকে আরো একভাবে লেখা যেতে পারতঃ

F = dp / dt, (১৭)

যেখানে p অক্ষরটি বোঝায় ভরবেগ বা momentum. আধুনিক বিজ্ঞানের দিক থেকে চিন্তা করলে কিন্তু (১৬)-এর চাইতে (১৭)টিই বেশি শক্তিশালী, কারণ এটি অপরিবর্তিত থাকবে ভর গতির ওপর নির্ভরশীল হলেও, কিন্তু (১৬) থাকবে না। (আইনস্টাইনের গতিবিজ্ঞানের প্রথম পদক্ষেপটিই তো ছিল স্থান আর সময় উভয়কে গতিনির্ভর করে ফেলা, যার ফলে ভর বেচারিকেও গতির মেজাজ অনুযায়ী ব্যবহার করা শিখতে হয়।)

পাঠককে যে জিনিসটা এখনো বলা হয়নি সেটা হলো ‘গতি” শব্দটির গাণিতিক সংজ্ঞা কী। ক্যালকুলাস বের হওয়ার আগে আসলে কোনো সঠিক সংজ্ঞা ছিলও না। গতির সঙ্গে নিউটনের ফ্লাক্সিয়ন আইডিয়াটির একটা ঘনিষ্ঠ সম্পর্ক আছে, সেটা অনুমান করা শক্ত নয়। এবং নিউটন ঠিক তা-ই করলেন। যে মুহূর্তে তিনি বুঝতে পারলেন যে তাইতো, গতি তো ফ্লাক্সিয়ন ছাড়া কিছু নয়, তৎক্ষণাৎ যেন তিনি দিব্যবাণী-প্রাপ্ত হয়ে লিখে ফেললেনঃ

v = dx/dt (১৮)

এখানে x হলো একটা বস্তুর অবস্থান, বা দূরত্ব কোনো কেন্দ্রবিন্দু থেকে, যেমন ডেকার্টের ভূমিস্থ অক্ষরেখা।

0————x———-→x – axis

সে হিসেবে নিউটনের দ্বিতীয় সূত্রটি দাঁড়ায়ঃ

F = d²x/dt²,

বা

F = (d/dt) (dx/dt), (১৯)

অর্থাৎ ত্বরণ হলো অবস্থানের দ্বিতীয় অন্তরকলন (second derivative with respect to time). আজকে এগুলো ডালভাত আমাদের কাছে। সে যুগে ছিল রীতিমতো বিপ্লব।

আমাদের আজকের আলোচনার মূল বিষয় থেকে খানিক ভিন্ন দিকে চলে যাওয়া হচ্ছে হয়তো, তবে আশা করি, নেহাত অপ্রাসঙ্গিকও মনে হবে না পাঠকের কাছে।

ক্যালকুলাসের জন্ম

ফ্লাক্সিয়ন (fluxion) শব্দটির আক্ষরিক অর্থ ‘প্রবহণ’ বা ‘পরিবর্তন’-যা ক্রমাগত বইছে, পরিবর্তিত হচ্ছে। আইডিয়াটি কী প্রসঙ্গে উদয় হয়েছিল ২৪ বছর বয়স্ক যুবকের মস্তিষ্কে জানি না, কিন্তু এর প্রয়োগ যে গণিত আর বিজ্ঞানকে আগাগোড়া বদলে দিয়েছিল, তাতে কোনো সন্দেহ নেই। দুঃখের বিষয় যে একে গণিতে ব্যবহারযোগ্য করার উদ্দেশ্যে যে গাণিতিক সংকেত বা প্রতীক তিনি ব্যবহার করেছিলেন, সেটা এমনই বিদঘুটে আর ব্যবহার-অযোগ্য ছিল যে একমাত্র তিনি এবং তাঁর কিছু ভক্ত ব্রিটিশ গণিতবিদ ছাড়া আর কেউ ব্যবহার করেছিলেন কি না সন্দেহ। এখানে বিজ্ঞানের গাণিতিক ভাষার একটা মৌলিক সত্য উল্লেখ করার লোভ সামলাতে পারছি না। সেটা হলো এই ‘প্রতীকের’ব্যাপারটি। তত্ত্বের সাথে সেই তত্ত্ব প্রকাশের ভাষাকেও কিন্তু বিজ্ঞানমাফিক হতে হয়, যাতে প্রথমত তার একটা যৌক্তিক সংগতি থাকে, দ্বিতীয়ত থাকে সহজ ব্যবহারযোগ্যতা, তৃতীয়ত থাকে পরবর্তীকালের গবেষকদের জন্য ভাবসম্প্রসারণ বা অধিকতর সর্বজনীনতার পথে অগ্রসর হবার সহজ পন্থা। উদাহরণস্বরূপ ওপরের (১৬) আর (১৭)-এর পার্থক্যটা লক্ষ করুন। একই সমীকরণ, আইনস্টাইনের আগ পর্যন্ত। আইনস্টাইন এবং তাঁরও আগেকার দু-চারজন গবেষকের জন্য (১৬)-এর চেয়ে (১৭)-ই ছিল বেশি মূল্যবান। তবে ষোড়শ শতাব্দীর শেষের দিকে ব্রিটেনে বসে কাউকে ক্যালকুলাস শিখতে হলে নিউটনের সেই কিম্ভূতকিমাকার প্রতীকই ব্যবহার করতে হতো। সৌভাগ্যবশত নিউটনের অল্প কয়েক বছর পর প্রায় একই আইডিয়া জন্ম নিয়েছিল ইউরোপের আরেক মনীষীর মাথায়, যাঁর নাম গটফ্রিড লিবনিজ (১৬৭৬- ১৭১৬)। জার্মানির এই আশ্চর্য প্রতিভাধর ব্যক্তিটি গণিতে যতটা পারদর্শী ছিলেন তার চেয়েও বেশি ছিলেন দর্শনশাস্ত্রে। এমনকি পদার্থবিজ্ঞানেও যথেষ্ট অবদান রেখে গেছেন তিনি। ক্যালকুলাসের ল আবিষ্কারক যে নিউটন তাতে কারো কোন সন্দেহ নেই (সনতারিখ মেলালেই তো বের হয়ে যায় সেটা), প্রশ্ন হল লিবনিজ কি নিউটনের আবিষ্কারের কথা শোনার আগে নিজে থেকেই ভেবেছিলেন কিনা। যাই হোক, এ বিষয়েও কোনো সন্দেহ নেই যে লিবনিজ যে প্রতীক সঙ্কেত ব্যবহার করেছিলেন সেটা ছিল সত্যিকার ব্যবহারযোগ্য সংকেত, এবং এই অধ্যায়ে এযাবৎ যেসমস্ত প্রতীক ব্যবহৃত হয়েছে, তার সব কটিই তাঁরই প্রবর্তিত প্রতীক। লিবনিজের চিন্তায় dx, dy, dt-এগুলো হলো সেই ‘ক্ষুদ্রাতিক্ষুদ্র’ সংখ্যা, যাকে গাণিতিক ভাষায় বলা হয় infinitesimal, যা স্বয়ং নিউটন সাহেবও খুব একটা সুদৃষ্টিতে দেখতেন না এবং যা নিয়ে শতাব্দীর পর শতাব্দী তর্কযুদ্ধ চলেছে তাত্ত্বিকদের মাঝে। কিন্তু লিবনিজ নির্দ্বিধায় তা গ্রহণ করে নিয়েছিলেন, এবং তার পূর্ণ সুযোগ নিয়ে গণিতের সম্পূর্ণ নতুন একটা শাখা তৈরি করে বিজ্ঞান আর গণিতকে তুমুল বেগে চলমান হয়ে উঠতে সাহায্য করেন। তাইতো বলি, আইডিয়াই পৃথিবী বদলায়। মানুষ চলে যায়, কিন্তু তার আইডিয়া থাকে, যদি তা থাকবার মতো হয় আদৌ।

এবার দুটি-একটি উদাহরণ দিয়ে ব্যাখ্যা করা যাক নিউটন কিভাবে তাঁর ‘ফ্লাক্সিয়ন’ দ্বারা অনেক অজানা বা কঠিন জিনিসের সহজ সমাধান দিতে পেরেছিলেন। প্রথমেই নেয়া যাক যা পাঠক আগেই দেখেছেন: সেই সমদ্বিবাহু সমকোণী ত্রিভুজটি — ক থেকে খ, ভূমিতে, খ থেকে গ লম্বালম্বি—একই দৈর্ঘ্য দুটি রেখারই। কগ এই অতিভুজটির ঢাল আমরা জ্যামিতির কাছ থেকেই পেয়েছি, ১। এবার দেখা যাক আমাদের নতুন শেখা ক্যালকুলাস কী দেয় এবং কত সহজে। ডেকার্টের বীজগাণিতিক জ্যামিতি আমাদের দিচ্ছেঃ

y = x, (২০)

কগ-এর সমীকরণ—ক্যালকুলাস ব্যবহার করতে হলে এটি অপরিহার্য। এবার x বিন্দু থেকে অত্যন্ত ক্ষুদ্র একটি দূরত্ব নিন, যেমন Δx, এবং সেখানে y -এর যে পরিবর্তন সেটাকে বলুন Δy তাহলে (২০) আমাদের দিচ্ছে, কগ রেখাটিতে দুটির সম্পর্কঃ Δy = Δx যার ফলে এ বিন্দুটিতে রেখাটির ঢাল হলো ১। যেহেতু ১ সংখ্যাটি কখনো বদলাবার নয়, এক বিন্দু থেকে আরেক বিন্দুতে যেতে সেহেতু রেখার ঢালেও কোনো পরিবর্তন হবে না। সুতরাং সমস্ত রেখাটির একই ঢালঃ ১, যা আগেরটির সঙ্গে হুবহু মিলে যাচ্ছে।

ছোট বাচ্চাকেও শেখানো যায়, তাই না? ছোট বাচ্চা হয়তো যেটা শিখতে পারবে না চট করে সেটা হলো একই উদাহরণ প্রয়োগ করে ত্রিভুজটির ক্ষেত্রফল, যা ৩২ বর্গ একক বলে আগেই আমরা জেনেছি, তা বের করা ক্যালকুলাসের সাহায্যে। প্রথমত ভূমিটিকে সমান n ভাগে ভাগ করুন, n-কে যথেষ্ট বড় ধরনের সংখ্যা হতে হবে, যে-কোনো বড় সংখ্যা হলেই চলবে আপাতত। তাহলে প্রতিটি ক্ষুদ্র অংশের দৈর্ঘ্য দাঁড়াল 8/n. এবার । -সংখ্যক অংশের দূরত্বে, অর্থাৎ মূল ক থেকে যার দূরত্ব হচ্ছে 8r/n, সেখানে লম্বের দৈর্ঘ্যও সেই একই- 8r/n.সুতরাং সেখানে দাঁড় করানো ছোট একটি চতুর্ভুজের ক্ষেত্রফল হচ্ছে দৈর্ঘ্য×লম্ব, যার অর্থ, (8r/n) ×(8/n) = 64r/n². এখন আমরা । -কে ক থেকে খ বিন্দুতে নিয়ে যাব অর্থাৎ 0 থেকে n পর্যন্ত। সুতরাং ত্রিভুজটির আনুমানিক ক্ষেত্রফল দাঁড়াচ্ছেঃ

Area = 64(1+2+3+….+n) / n² (২১)

(23) ওপরের 1 থেকে n অবধি সন্মান্তর রাশিটির যোগফল স্কুলের দশ-বারো বছরের ছেলেমেয়েদেরও শেখা। সেটি ধার করে লেখা যায়ঃ

Area = 32(n(n + 1)) / n² = 32+32/n. (২২)

এযাবৎ একবারও কিন্তু লিমিট বা infinitesimal-জাতীয় শব্দ ব্যবহার করা হয়নি। (২২) পর্যায়ে সেটি করা হবে। ৩২/n-কে যত ছোট করা সম্ভব করে যান, (যার মানে, n যাবে অসীম লিমিটে) যতক্ষণ না তার অস্তিত্বই প্ৰায় লোপ পেয়ে যায়। একেই তো বলি লিমিট, infinitesimal,তাই না? এই লিমিটে তাহলে 32/ n সংখ্যাটির কী দশা দাঁড়াচ্ছে? প্রথম সংখ্যাটির তুলনায় একেবারেই তুচ্ছ। অর্থাৎ এর লিমিট হচ্ছে )। এভাবেই ক্যালকুলাসে সমাকলন শাখা আমাদের আয়ত্তের মধ্যে এনে দেয় সমতল ভূমির ক্ষেত্রফল বের করার সহজ পদ্ধতি। ত্রিভুজটির ক্ষেত্রে এ পথে যাওয়ার দরকার ছিল না, কিন্তু সরলরেখার চেয়ে হাজার জটিল রেখার ক্ষেত্রে ক্যালকুলাস ছাড়া অন্য কোনো পথ এখনো পর্যন্ত কারো জানা নেই।

কোনো কোনো পাঠকের বিচারে ওপরের উদাহরণগুলো নেহাত ছেলেখেলা মনে হতে পারে। তাই আগের সেই অধিবৃত্তের উদাহরণটি নিয়ে ক্যালকুলাসের কী দারুণ শক্তি তার একটা আবছা আভাস দেবার চেষ্টা করব। ধরা যাক অধিবৃত্তটির সমীকরণ হলোঃ

y = x² (২৩)

সুতরাং

y + Δy = (x + Δx)²

= x² + 2xΔx + (Δx)² (২৪)

এখন (২৪) থেকে (২৩) বিয়োগ করুন।

থাকছেঃ Δy = 2xΔx + (Δx)²

যাকে Δx দিয়ে ভাগ করে পাইঃ Δy / Δx = 2x + Δx (২৫)

এ পর্যায়ে লিমিটের সাহায্য ছাড়া উপায় নেই। Δx আর Δy উভয়কে শূন্যের দিকে পাঠালে ডান দিকে কী থাকে? শুধু 2x, কারণ Δx তো শূন্যেই চলে যাচ্ছে। তার অর্থ, এই (x, y) বিন্দুটিতে রেখাটির ঢাল হলো 2x. গণিতের প্রচলিত সাংকেতিক ভাষাতে এটিকে এভাবে ব্যক্ত করা হয়ঃ

dy / dx = lim _Δx→0 Δy/Δx = 2x (২৬)

ধারণা করা যায়, এভাবেই নিউটন তাঁর জীবনীতে বর্ণিত স্পর্শক-পদ্ধতি আবিষ্কার করেছিলেন।

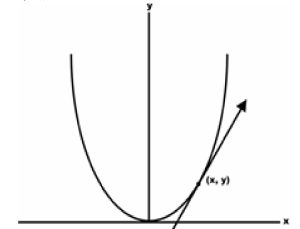
এবার এই রেখাটিরই নিচের এলাকাটির ক্ষেত্রফল বের করার চেষ্টা করব লিমিটের সাহায্যে। আগেকার সেই ত্রিভুজের মতো এটিরও ভূমি ধরা যাক ক থেকে ৮ একক দূরত্বে খ পর্যন্ত বিস্তৃত। তবে আগের মতো খ থেকে গ অবধি যে লম্ব রেখাটি তার দৈর্ঘ্য বদলে গিয়ে দাঁড়াবে ৮-এর বর্গে, অর্থাৎ ৬৪।

কথা হলোঃ এই যে বৃদ্ধিপ্রাপ্ত ও বাঁকা রেখা-পরিবেষ্টিত এলাকাটি, তার ক্ষেত্রফল কি? আগের সেই ত্রিভুজটির মতো করেই ভূমিকে ভাগ করব n-সংখ্যক একক ডানে এর দূরত্ব দাঁড়াচ্ছে 8r/n, এবং ক্ষুদ্র অংশে যাতে মূল থেকে x সেখানে তার উচ্চতা হলো (8r/n)² = 64(r/n)².সুতরাং মোটমাট গোটা এলাকাটির একটা আনুমানিক পরিমাপ লেখা যায় এভাবেঃ

Area = ∑(64(r/n)²) (8/n)

= (512/n³) {l +2² + 3² +……+ n² (২৭)

{ }বদ্ধ রাশিগুলোর যোগফলের জন্য স্কুলপাঠ্য বীজগণিত বইয়ের সাহায্য নিতে হবে। এটা হলোঃ

(n(n+1)(2n+1))/6

বিশ্বাস হচ্ছে না বুঝি? n = 1,2,3,…. এরকম ছোট ছোট সংখ্যা নিয়ে গুনে দেখুন মেলে কি না। ওই যে বললাম, গণিতের লোকেরা ভীষণ কুঁড়ে, তাদের ফর্মুলা না হলে চলে না। তবে ফায়দাটা লক্ষ করুন। এবার যে সংখ্যাটি পাচ্ছি আমরা এই ক্ষেত্রফলের জন্য সেটা হলোঃ

Area = 512n(n+1)(2n+1)/6n³ (২৮)

এইখানে এসে আমরা সেই একই কাজ করব, লিমিট নেব n-কে অসীম যাত্রায় পাঠিয়ে, মানে 1/n_কে শূন্যের দিকে নিয়ে।

শেষমেশ পাচ্ছি ৫১২/৩। এলাকাটির বর্গফল। ক্যালকুলাসের সমাকলন নিয়ম দিয়ে কষতে গেলে এত সময় লাগবে না এবং একই ফল পাওয়া যাবে।

ক্যালকুলাস নতুন বিদ্যা হলেও এরকম খণ্ড খণ্ড ভাগে বিভক্ত করে সেগুলোকে একসাথে যোগ করে ক্ষেত্রফল বের করার পদ্ধতি অতি পুরাতন সেটা তো আগেই বলেছি। পুরনো জ্ঞানের ওপর ভর করেই তো নতুন জ্ঞান জন্ম নেয়। নিউটন সেটা নিজেই স্বীকার করে গিয়েছেন।

ক্যালকুলাসের জনক কে?

কলন-শাস্ত্রের জনক কে তা নিয়ে তুমুল বিতর্ক সৃষ্টি হয়েছিল সেকালের ইউরোপে। এক পক্ষ বলে নিউটন, আরেক পক্ষ লিবনিজ। অনেকটা বাংলাদেশের ‘জাতির জনক’ সমস্যাটির মতো। অবশ্য বাংলাদেশের স্বাধীনতার ইতিহাস যারা ভাল করে জানে তাদের মনে এ নিয়ে কোনো সমস্যাই নেই, সমস্যা হলো যখন একদল আরেক দলকে ঘায়েল করার চেষ্টায় গোটা ইতিহাসটাকেই বিকৃত করে ফেলে। কিন্তু সপ্তদশ শতাব্দীর ক্যালকুলাস বিতর্কে ব্যাপারটি অত সাদামাটা ছিল না। সমস্যার গোড়াতে কিন্তু, অনেকের মতে, দায়ী ছিলেন নিউটন নিজেই। তাঁর সেই অতিমাত্রিক গোপনীয়তা, সেই স্বভাবসিদ্ধ সবাইকে সন্দেহের চোখে দেখার প্রবণতা, পাছে না কেউ কিছু চুরি করে নেয় তাঁর কাছ থেকে, সেই ভয়ে সব সময় সতর্কতা অবলম্বন করা। সেসব কারণে ক্যালকুলাসের ওপর তাঁর যুগান্তকারী ফলাফলগুলো, আবিষ্কারের বহু বছর পর, ১৬৯৩ খ্রিষ্টাব্দে, প্রকাশ করেছিলেন। ওদিকে লিবনিজ তাঁর নিজের আইডিয়াগুলো পেয়েছিলেন ১৬৭৫ সালে। তারপর সেগুলোকে ভালো করে সাজিয়ে-গুছিয়ে প্রকাশযোগ্য করে ছাপতে দিয়েছিলেন ১৬৮৪ সালে। খবর পেয়ে নিউটন ভাবলেন, বেটা নিশ্চয়ই তাঁর রেজাল্ট চুরি করে নিজের নামে ছাপিয়ে দিয়েছে। অভিযোগটা যে একেবারে দুনিয়াছাড়া গাঁজাখুরি ব্যাপার ছিল তা-ও বলা চলে না। লিবনিজ পেশাতে ছিলেন আইনজ্ঞ, ফরাসি নাগরিক পিয়ের ফার্মার মতো, এবং ফার্মারই মতো দারুণ বড়লোকের ছেলে, বিত্তবান ও প্রভাবশালী। তিনি পেশাগত কারণেই ১৬৭৩ থেকে ১৬৭৬ সাল পর্যন্ত পাকা তিন বছর কাটিয়েছিলেন লণ্ডনে। তার আগে নিউটনের সঙ্গে নিয়মিত যোগাযোগও হতো চিঠিপত্রের মাধ্যমে। নিউটনের ‘ফ্লাক্সিয়ন’ তত্ত্বের খবর হয়তো তাঁর জানা ছিল, কিন্তু তার কোনো প্রভাব পড়েছিল কি না তাঁর ওপর সে কথা কারো পক্ষেই হলফ করে বলা সহজ নয়। নিউটন তো ধরেই নিলেন যে লিবনিজ সাহেব লণ্ডনে থাকাকালে কোনো-না-কোনোভাবে বের করে নিয়েছে তাঁর গোপন আবিষ্কার। পয়সাওয়ালা জার্মান দুলালদের কি কোনো বিশ্বাস আছে? সে কী ঝগড়া দুজনের ! নিউটন যেমন ছিলেন সন্দেহপ্রবণ, লিবনিজ ছিলেন একটু উদ্ধত প্রকৃতির, ছেড়ে দেবার পাত্র মোটেও ছিলেন না তিনি।

সেই ঝগড়া শেষ পর্যন্ত সারা ইউরোপের আবহাওয়াকে বিষাক্ত করে তোলে। ব্রিটেন আর ইউরোপ কেউ কারো মুখদর্শন করবে না এমন অবস্থা।

বেশ কয়েক শতাব্দী লেগেছে দুপক্ষের মাথা ঠাণ্ডা হতে। ইতোমধ্যে আসল ক্ষতিটা হয়েছে ব্রিটেনেরই। ইউরোপ যেখানে আধুনিক গণিতের বিবিধ শাখাতে শাঁই শাঁই করে এগিয়ে চলেছে, ব্রিটেন তখন নিউটনের অন্ধ অনুকরণে গতানুগতিকতার শেকলে আবদ্ধ হয়ে থাকে। সেই নিউটনীয় ধারারই ঢেউ লেগেছিল ভারতবর্ষসহ সমগ্র ব্রিটিশ সাম্রাজ্যে। সম্ভবত সে কারণেই ভারতের গণিতচর্চাতে সত্যিকার কোনো গতি সৃষ্টি হয়নি গত কয়েক শতাব্দী। একই ধরনের সেকেলে ধারায় গৎবাঁধা জিনিস নিয়ে মগ্ন থেকেছি, এমনকি দেশ স্বাধীন হবার পরও।

রাজনীতির মতো গণিতের ইতিহাসও কম বিচিত্র নয়।

গণিতের কলনশাস্ত্রের জন্মকাহিনির একটা সংক্ষিপ্ত বর্ণনা দেওয়া হলো। পরের অনুচ্ছেদে যাব সেই অস্বস্তিকর 0/0_এর প্রসঙ্গে, যাকে নিউটন বা লিবনিজ কেউই সরাসরি মোকাবিলা করতে সাহস পাননি। কিন্তু তার আগে একটু পরচর্চা করা যাক, মানে উচ্চমানের গাণিতিক পরচর্চা।

একের কাম অন্যের নাম

১৬৬১ খ্রিষ্টাব্দে ফ্রান্সের এক প্রতিপত্তিশালী অভিজাত পরিবারে জন্মগ্রহণ করেন ফ্রাঁসোয়া-আঁতোয়া দ্য লোপিতাল। (Guillaume – Francois – Antoine de 1’Hopital)। আমাদের উপমহাদেশের বইপুস্তকে কখনো কখনো লেখা হয় L’Hospital, যার ফলে এর উচ্চারণটিও ল’হস্পিটাল হয়ে গেছে অধিকাংশ জায়গায় (আমরাও ছাত্র থাকাকালে এই উচ্চারণই শিখেছি)। ছোটবেলায় স্কুলে পড়ার সময় থেকেই অঙ্কের প্রতি ভীষণ একটা আকর্ষণ জন্মায় লোপিতালের। সম্ভবত পারিবারিক কারণেই প্রাপ্ত বয়সে অঙ্কে না গিয়ে তাঁকে যেতে হয়েছিল সেনাবিভাগে। অশ্বারোহী বাহিনীর ক্যাপ্টেন পর্যন্ত পদোন্নতি হয়েছিল তাঁর। কিন্তু অচিরেই তাঁর মন ছুটে যায় সেই পুরনো প্রেম, অঙ্কের দিকে। সব ছেড়েছুড়ে দিয়ে তিনি মজে গেলেন অঙ্ক নিয়ে। কিন্তু দীর্ঘকাল চর্চা না থাকাতে সবকিছু নতুন করে শিখবার উদ্যোগ নিতে হলো। সারা মুল্লুকের সবচেয়ে নামকরা শিক্ষক খুঁজে পেলেন একজন, নাম ইউহান বার্নলি (১৬৬৭-১৭৪৮)। আদিবাস বেলজিয়াম থেকে সুইজারল্যান্ডে চলে আসা বার্নলি-পরিবার ধনসম্পদে খুব একটা সচ্ছল ছিলেন না, কিন্তু ধনী ছিলেন মেধাসম্পদে। তিনি এবং বড় ভাই জ্যাকব বার্নলি (১৬৫৪-১৭০৫), দুজনই ছিলেন সে যুগের শীর্ষস্থানীয় ইউরোপিয়ান গণিতজ্ঞ। ইউহান বার্নলির ছেলে ড্যানিয়েল বার্নলি (১৭০০-১৭৮২) ছিলেন আরেক মহিরুহ‘কিনেটিক থিওরি অব গ্যাসেস’ নামক পদার্থবিদ্যার নতুন একটি শাখাই সৃষ্টি করে ফেলেছিলেন তিনি। ড্যানিয়েলের বাপ-চাচা দুজনেরই নাম গণিতশাস্ত্রের সর্বত্র। সংখ্যাতত্ত্ব (Number Theory) থেকে পরিসাংখ্যিক গণিত (Probability Theory) সবকিছুতেই দুজনের কারো না কারো হাত ছিল। ইউহানের বিশেষ রকম ব্যুৎপত্তি ছিল লিবনিজের নতুন গণিত ক্যালকুলাসে। কিন্তু স্বাধীনভাবে গবেষণাকর্মে মগ্ন থেকে জীবন যাপন করার মতো আর্থিক সচ্ছলতা ছিল না তাঁর। তাই লোপিতাল যখন তাঁকে শিক্ষক নিযুক্ত করার প্রস্তাব দেন, তিনি সানন্দে সেটা গ্রহণ করে নেন। লোপিতাল কোনো গাধা ছাত্র ছিলেন, তা মোটেও নয়। চট করে সব শিখে ফেলতে পারতেন।

প্রথম থেকেই তিনি বার্নলির শেখানো ক্যালকুলাসের প্রতি দারুণ আকৃষ্ট হয়ে পড়েন। বিষয়টির প্রতি এতই ঝোঁক হয়ে গেল তাঁর যে শিক্ষকের কাছে প্রস্তাব পেশ করলেন যে ক্যালকুলাস-বিষয়ক যত কাজকর্ম আছে তাঁর সবগুলোই তিনি কিনে ফেলতে প্রস্তুত, যত টাকা চান তিনি ততই দেবেন। আর্থিক অনটনে পড়া ইউহান বার্নলি ভাবলেন, ক্ষতি কী, তাঁর মাথায় তো আরো নতুন আইডিয়া আসবে, কিন্তু এতগুলো টাকা তো আসবে না এত সহজে। তিনি রাজি হয়ে গেলেন ছাত্রের প্রস্তাবে। একটা শর্ত ছিল ছাত্রের, কাগজগুলো যদৃচ্ছ ব্যবহারের অধিকার থাকবে তাঁর, অর্থাৎ বার্নলির কাগজপত্রের যা কিছু ফলাফল তার ওপর সমস্ত স্বত্বাধিকার তিনি স্বেচ্ছায় সঁপে দিচ্ছেন লোপিতালকে। সেই কাগজগুলোতে যে সমস্ত ফলাফল ছিল, তার সঙ্গে নিজের কিছু চিন্তাভাবনা যোগ করে আঁতোয়া লোপিতাল রীতিমতো একটা বই লিখে ফেললেন ক্যালকুলাসের ওপর – Analyse des infiniment petits নাম দিয়ে। সে বই প্রকাশিত হয় ১৬৯৬ সালে ক্যালকুলাস-শাস্ত্রের ওপর পৃথিবীর প্রথম পাঠ্যপুস্তক। সে বইতে বার্নলির একটি গুরুত্বপূর্ণ রেজাল্ট ছিল যার ওপর তাঁর স্বত্ব ছিল না বলে সেটি ‘লোপিতালস রুল’ বলে পরিচিত হয়ে এসেছে দুনিয়াসুদ্ধ ছাত্রছাত্রী আর শিক্ষক-অধ্যাপকদের কাছে। নিজের আবিষ্কৃত রেজাল্ট ব্যবহার করে নেহাত টাকার জোরে অন্য এক ব্যক্তি খ্যাতি অর্জন করছে সেটা দেখে বার্নলির যে খুব ভালো লাগছিল না সেটা তো সহজেই বোঝা যায়, কিন্তু চুক্তিবদ্ধ হওয়ার ফলে মুখ ফুটে কিছু বলারও উপায় ছিল না বেচারার। তারপর যখন লোপিতাল মারা যান ১৭০৪ সালে, তখন আর চুপ করে থাকার প্রয়োজন বোধ করলেন না, ফাঁস করে দিলেন আসল ঘটনাটা। সে সময় লোপিতাল এতই বিখ্যাত হয়ে গিয়েছিলেন যে বার্নলির কথায় কেউ কান দেয়নি। না দেবার আরেকটা কারণও ছিল। তিনি নিজেও এরকম একটি কুকর্ম করেছিলেন একবার, তা-ও নিজের আপন ভাইয়ের সঙ্গে। বড় ভাইয়ের একটা কাজকে নিজের বলে চালিয়ে দিয়েছিলেন। বড় কথা, দিতে গিয়ে ধরাও পড়েছিলেন। তার ফলে তাঁর বিশ্বাসযোগ্যতা হারিয়ে যায়। যা-ই হোক, তাঁর মৃত্যুর পর পুরনো চিঠিপত্র ঘেঁটে পরবর্তীকালের গবেষকেরা বুঝতে পেরেছিলেন যে আসলেই কাজটা ছিল ইউহান বার্নলির। কিন্তু তত দিনে লোপিতাল নামটিই আঠার মতো লেগে যায় সূত্রটির সঙ্গে।

এবার দেখা যাক কী সেই সূত্র। ধরা যাক x/x ভগ্নাংশটি। x যদি ০ না হয় তাহলে এর একটা অর্থ আছে—ওপরে নিচে কাটাকুটি করে ফল পেয়ে যাই ১। কিন্তু x যদি 0 হয় তাহলে তো বিপদ—ভগাংশটি অর্থ হারিয়ে একটা অনির্ণেয় বর্জ্য দ্রব্য হয়ে দাঁড়ায়। কোন মানেই থাকে না তার। যুগ যুগ ধরে বড় বড় পণ্ডিতেরা যমের মতো এড়িয়ে গেছেন একে। দার্শনিকেরা তিরস্কার করেছেন যারা এটা নিয়ে চিন্তাভাবনা করার সাহস পায়। নিউটন আর লিবনিজের মতো নবযুগের দিগদিশারি গণিতবিদেরাও দূরত্ব বজায় রেখেছেন এর থেকে। কিন্তু লোপিতাল তাতে দমে যাননি (ঐতিহাসিক কারণে লোপিতালকেই কৃতিত্ব দিতে হচ্ছে যদিও সকলেরই জানা হয়ে গেছে এর মাঝে যে মূল আবিষ্কারক তিনি নন, ইউহান বার্নলি)। তিনি বরং উলটো বললেন যে ভগ্নাংশের মান 0/0 হলে ক্ষতি নেই, যদি ওপর-নিচ দুটি ফাংশনই ‘কলনযোগ্য’ (differentiable) হয়, এবং অন্তরকলনের ফলে যদি নতুন ফাংশন দুটি একটা সুনির্দিষ্ট ফলাফল দেয়, x = 0 বসাবার পর। অবশ্য যদি এমন হয় যে দ্বিতীয় পর্যায়েও সেই একই অবস্থা দাঁড়াচ্ছে, অর্থাৎ 0/0 ভগ্নাংশ দিচ্ছে, তাহলে পূর্ববর্ণিত সেই একই প্রক্রিয়া দ্বিতীয়বার চালানো যাবে। এবং এভাবে যতবার দরকার ততবারই যাওয়া যাবে, যতক্ষণ না শেষমেশ একটা সিদ্ধান্তে পৌঁছানো সম্ভব, হয় কোনো সসীম সংখ্যায় যাবে, নয়তো অসীম সংখ্যাতে; কিংবা কোনো লিমিটেই যাবে না। সবগুলোরই পেছনে কতগুলো আইনকানুন আছে, যেমন লিমিট থাকা বা না থাকা, কলনযোগ্য হওয়া বা না হওয়া (না হলে সেখানেই থেমে যেতে হবে), ইত্যাদি।

ফিবোনাচি, না বিরহাঙ্ক ?

ইংরেজিতে প্লেজিয়েরিজম (plagiarism) বলে একটা কথা আছে, যার বাংলা তরজমা, ভদ্র ভাষাতে, ‘কুম্ভিলকতা’, অনতিভদ্রতে সোজা ‘চৌর্যবৃত্তি’। তবে এটা সাধারণ পকেটমারা বা সিঁদকাটা চৌর্যবৃত্তি নয়, বুদ্ধিজগতের শিক্ষিত চৌর্য। জ্ঞানবিজ্ঞানের জগতে এর মানে দাঁড়ায়: একজনের গবেষণালব্ধ মৌলিক কাজ আরেকজন তার নিজের বলে চালিয়ে দেওয়া, এবং ফলত রীতিমতো নাম করে ফেলা। এরকম ঘটনা অহরহই ঘটত আগেকার দিনে। ছাত্রের লেখা অভিসন্দর্ভের পুরো কৃতিত্বটাই হয়তো অবেক্ষক সাহেব আত্মসাৎ করে ছাপিয়ে দিলেন নামকরা জার্নালে, আর ছাত্র বেচারা ঘরে বসে রাগে-দুঃখে নিজের চুল ছেঁড়া ছাড়া আর কোনো পথ খুঁজে পেল না, এধরনের অবিশ্বাস্য ঘটনাও যে ঘটেনি তা নয়। তবে বর্তমান যুগের ‘চৌর্যবৃত্তি’ একটু ভিন্নরকম। ইন্টারনেটের কল্যাণে যেহেতু কেউ কারো কাছ থেকে সহজে কিছু লুকিয়ে রাখতে পারে না, সেহেতু ‘চুরি’টা হয় প্রধানত সেই ইন্টারনেটেরই কাছ থেকে। যেমন, গুগলের মারফতে ইন্টারনেট থেকে একটা তথ্য ‘ধার’ করার পর গবেষণাপত্রে সেই তথ্যসূত্রটি বেমালুম চেপে গিয়ে নিজের বলে দাবি করার চেষ্টা। মানবচরিত্রের এই ছোটখাটো হীনতাগুলো চিরকালই ছিল,চিরকাল থাকবেও। তবে উঁচুমানের গবেষক- সাধকদের মধ্যে এই দুর্বলতাগুলো খুব কমই দেখা গেছে। যা অনেক ক্ষেত্রেই ঘটেছে তা হলো একের কাজ সম্বন্ধে অন্যজন সম্পূর্ণ অনবহিত হয়েই তার নিজের কাজটি কোনো পত্রিকায় প্রকাশ করে ফেলেছেন, যদিও সেই একই কাজ হয়তো অন্য লোকটি অন্য কোনো দেশের অন্য কোনো পত্রিকায় তার আগেই প্রকাশ করে ফেলেছিলেন। সেটা ‘চৌর্যবৃত্তি’ নয়,এমনকি অনিচ্ছাকৃত ভুলও নয়,সেটা স্বাধীন ও যুগপৎ গবেষণা। দুজনেরই সমান অধিকার গবেষণার কৃতিত্ব দাবি করার।

একদিন আমাদের বিশ্ববিদ্যালয়ের বিভাগীয় অফিসের কফিরুমে বসে এক সহকর্মী বন্ধুর সঙ্গে আলাপ করছিলাম কফি খেতে খেতে। কথা উঠল ফিবোনাচি সংখ্যা নিয়ে (বিজ্ঞ পাঠকদের মনে আছে নিশ্চয়, ফিবোনাচিকে নিয়ে আমরা আলোচনা করেছি এই বইয়ের চতুর্থ অধ্যায়ে)। আমার (মী.র বন্ধুটি গণিতের বীজগণিত শাখার একজন বিশ্বমাপের পণ্ডিত। হেসে বললেন, আরে কিসের ফিবোনাচি। তার বহু আগেই ভারতীয় গাণিতিকরা করে গেছেন সেটা। বন্ধুটি চেকোশ্লাভিয়ার অভিবাসী,আমারই মতো দীর্ঘকাল ক্যানাডায়। তিনি একজন ইউরোপিয়ানকে ইতিহাসের পাতা থেকে সরিয়ে ভারতের এক হিন্দু গাণিতিককে বসিয়ে দেবেন সেটা একটু আশ্চর্যজনক মনে হতে পারে আমাদের কাছে, কিন্তু আসলে জ্ঞানবিজ্ঞানের জগতে এই সততাটুকু কাম্যই কেবল নয়,সচরাচর তা-ই দেখা যায়। ওর কাছ থেকে এর সূত্র কোথায় তার খবর নিয়ে আমি (মী.র) ইন্টারনেট থেকে পেলাম পরমানন্দ সিংহ নামক এক গাণিতিকের লেখা নিবন্ধ, যার শিরোনাম: The so-called Fibonacci Numbers in Ancient and Medieval India1o. লেখাটির ভূমিকাতে তিনি তার বক্তব্যের মূল বিষয়টি মোট পাঁচটি ভাষাতে ব্যক্ত করেছেনঃ ইংরেজি, ফরাসি,জার্মান,হিন্দি ও বাংলা। তার বাংলা অনুবাদটি এখানে হুবহু তুলে দিচ্ছি-

এল ফিবোনাচির (১২০২ খৃষ্টাব্দ) পূর্বে বিরহাঙ্ক (খৃঃ ৫০০- খৃঃ ৬০০ এর মধ্যে), গোপাল (১১৩৫ খৃষ্টাব্দের আগে), এবং হেমচন্দ্রের (১১৫০ খৃষ্টাব্দের নিকট) সকলেই তথাকথিত ফিবোনাচি সংখ্যা এবং তার নির্মাণ বিধির বর্ণনা করে গেছেন। নারায়ণ পণ্ডিত (১৩৫৬ খৃষ্টাব্দ)সামাসিক পঙক্তি, যার এক বিশেষ রূপ হচ্ছে ফিবোনাচি সংখ্যা, এবং বহুপদী গুণকের মধ্যে সম্বন্ধ স্থাপন করেছেন।

বিরহাঙ্ক বাবু ছিলেন সংস্কৃত কাব্যের ছন্দজ্ঞান বিশেষজ্ঞ, যা আমরা নই। বরং খোলসা করে বলা যায়,সংস্কৃত বা যেকোনো ভাষার কাব্যরচনা বিধি বিষয়টিতে এ বইয়ের লেখকদ্বয় রীতিমতো গণ্ডমূর্খ। অতএব নিচে যে আলোচনাটুকু নিবেদন করছি পাঠকের সুবিধা হবে ভেবে,তাতে যদি সুবিধার পরিবর্তে আরো ধাঁধার ভেতরে পড়ে যান পাঠক তাহলে আমাকে ক্ষমা করতে হবে।

পরমানন্দ মহাশয়ের ভূমিকা অনুযায়ী সংস্কৃত কাব্যে ছন্দের একমাত্রিক ধ্বনি বা স্বরকে (Syllable) বলা হয় ‘লঘু’,আর দ্বিমাত্রিক ধ্বনিকে বলা হয় ‘গুরু’ । ধরা হোক যে প্রথমটির ওজন ১,আর দ্বিতীয়টির ২। লেখক বলছেন যে,সংস্কৃত আর প্রাকৃত কাব্যে তিনপ্রকারের ছন্দরীতিঃ এক,বর্ণবৃত্ত,যাতে অক্ষর-সংখ্যা বদলাবে না,তবে ধ্বনি-সংখ্যা পারবে। দুই,মাত্রাবৃত্ত,যেখানে ধ্বনি-সংখ্যা অপরিবর্তিত,তবে অক্ষর-সংখ্যা বদলাতে পারবে। তিন,গণ বা গুচ্ছ-বৃত্ত,যেখানে একই গুচ্ছের ভেতর প্রথম বা দ্বিতীয়টির বৈশিষ্ট্য বজায় থাকবে,তবে গুচ্ছে গুচ্ছে ভিন্ন ভিন্ন বৈশিষ্ট্যের সমাবেশ থাকা সম্ভব। আমাদের বর্তমান আলোচনার জন্য দ্বিতীয়টিরই গুরুত্ব সবচেয়ে বেশি। এখানে তৃতীয়টি একেবারেই নিষ্প্রয়োজন বলে এর

প্রকাশকাল ও অন্যান্য তথ্যাবলীঃ Historia Mathematica, 12, pp 229-244,

আলোচনা স্থগিত রাখব—-এটা গণিতের বিষয় তত না, যতটা ছন্দ- বিন্যাসের।

প্রথমটির উদাহরণঃ

১ অক্ষর – ল (লঘু) বা গ (গুরু) মোট সংখ্যা ২ = ২

২ অক্ষর – লল,লঘ,ঘঘ, ঘল মোট সংখ্যা ৪ =২× ২

৩ অক্ষর – ললল,লগল,ললগ,লগগ,গগগ, গগল, গলগ, গগগ – মোট সংখ্যা ৮=২× ২× ২

সজাগ পাঠকের কাছে ধারাটি বেশ পরিষ্কারভাবেই ফুটে উঠেছে, তাই না? এখন যে কেউ বলে দিতে পারবে n অক্ষরবিশিষ্ট লাইনের মোট কটি সংখ্যা দাঁড়াবে: ২-কে n বার ২ দিয়েই গুণ করলে যা পাওয়া যায়। অর্থাৎ ৪ অক্ষর হলে ১৬ বার, ৫ হলে ৩২ বার,- এভাবে চলবে।

২, ৪, ৮, ১৬, —-এই সংখ্যামালাটি যে ফিবোনাচি রাশির সঙ্গে একেবারেই সম্পর্কহীন সেটা স্পষ্ট। তবে এটা যে গণিতে অন্য কোনো শাখার সঙ্গে সংশ্লিষ্টতাহীন তা কিন্তু মোটেও নয়। যেমন,একটা মুদ্রা একবার ছুড়লে হয় মাথা আসবে,নয় লেজ আসবে,অর্থাৎ ২টি সম্ভাব্য ফলাফল। ২ বার ছুড়লে ২× ২ =৪টি,৩ বার ছুড়লে ২× ২× ২=৮টি, —-অবিকল ওপরের উদাহরণটির মতো। এই মুদ্রা নিক্ষেপের উদাহরণটি কিন্তু কোনো ছেলেখেলা নয়, ,পরিসংখ্যান-শাস্ত্রের অত্যন্ত গুরুত্বপূর্ণ মডেল একটি। অতএব ছন্দ- ব্যাকরণের সঙ্গে গণিতের একাধিক শাখার ঘনিষ্ঠ সম্পর্ক রয়েছে। যা-ই হোক, বর্তমান নিবন্ধের পরিপ্রেক্ষিতে আমরা বর্ণ-বৃত্তের আলোচনাতে এখানেই যতি টানব।

দ্বিতীয়টির উদাহরণঃ

১ অক্ষর ল (গ সম্ভব নয়,কারণ গ’তে দুই মাত্রা), –মোট সংখ্যা ১

২ অক্ষর লল,গ— মোট সংখ্যা ২

৩ অক্ষর ললল,লগ,গল— মোট সংখ্যা ৩

৪ অক্ষর লললল,লগল,ললগ,গলল,গগ— মোট সংখ্যা ৫

৫ অক্ষর ললললল,লললগ,ললগল,লগলল, গললল,গলগ,গগল,লগগ— মোট সংখ্যা ৮

নিয়মটা নিশ্চয়ই বেশ পরিষ্কার হয়ে উঠছে? এবং এটাও নিশ্চয়ই প্রতীয়মান হয়ে উঠছে যে ডান দিকের সংখ্যাগুলোকে পাশাপাশি দাঁড় করালে দেখা যাবে এরা সেই ফিবোনাচি রাশি –

১, ২, ৩, ৫, ৮, ১৩,…

তার অর্থ কবিতার মাত্রাবৃত্ত ছন্দের সাথে গণিতের ফিবোনাচি রাশি ওতপ্রোতভাবে জড়িত। এবং যেহেতু এই সম্পর্কটি অত্যন্ত সরাসরি,এবং বিরহাঙ্ক বাবু ফিবোনাচি থেকে অন্তত ৬ শ’ বছর আগে এটি আবিষ্কার করেছিলেন,সেহেতু আমার মনে হয় ঐতিহাসিক ন্যায়বিচারের কথা ভেবে এই গুরুত্বপূর্ণ রাশিটিকে এখন থেকে বিরহাঙ্ক-ফিবোনাচি রাশি বলে অভিহিত করা উচিত।

আশা করি পাঠকদের কেউই ভাববেন না যে ফিবোনাচি সাহেব জেনেশুনেই বিরহাঙ্কের নামটি চেপে গিয়ে নিজের নামে চালিয়ে দিয়েছিলেন। না,আমাদের মনে হয় না যে উনি ওরকম অসাধু ছিলেন। যদি হতেন তাহলে তিনি কেন গায়ে পড়ে ভারতীয় গণিত প্রচার করার উদ্দেশ্য নিয়ে রীতিমতো একটা বই লিখে ফেলবেন? শুধু তা-ই নয়, রাশিটি যে ফিবোনাচির নামে ভূষিত হয়ে গেছে সেটা কিন্তু তিনি নিজে করেননি,নামকরণটি করেছিলেন এডওয়ার্ড লুকাস (১৮৪২-৯১)নামক এক অনতিবিখ্যাত গাণিতিক ফিবোনাচির মৃত্যুর প্রায় সাড়ে ছ’শ বছর পর। না,এটা চোর্যবৃত্তির ব্যাপার নিশ্চয়ই নয়,নেহাত অনবহিততার বিষয়।

আরেকটি উদাহরণ নেওয়া যাকঃ x/x² ওপরে-নিচে দুজায়গাতেই শূন্য আসছে x যখন 0 হয়। সৌভাগ্যবশত x এবং x² দুটিরই ডেরিভেটিভ আমরা অনায়াসে বের করে ফেলতে পারি। x-এর ডেরিভেটিভ হলো 1, আর x² এর 2x- এটা আগের পর্বের একটি উদাহরণ থেকে নেওয়া। সুতরাং লোপিতালের দাওয়াই অনুযায়ী পাওয়া যাচ্ছেঃ 1/2x. মহা বিপদ ! ওপরে 1, যা অপরিবর্তনীয়, আর নিচে 2x, যা x = 0 -তে () ই থাকে। সুতরাং আমরা পাচ্ছিঃ lim _x→0 (1/2x) → অসীম,

যার কোনো নির্দিষ্ট লিমিট নেই, ধনাত্মক অসীম হতে পারে, আবার ঋণাত্মক অসীমও হতে পারে, আগেকার সেই উদাহরণটির মতো। এক্ষেত্রে সিদ্ধান্ত দাঁড়াবে, এর কোনো লিমিট নেই, x যখন 0-এর দিকে যায়।

পুরো নিয়মটা হলো এরকমঃ

দুটি ফাংশন নিনঃ ƒ(x) আর g(x), এবং ƒ(x) কে ভাগ করুন g(x) দিয়ে। অর্থাৎ ƒ(x)/g(x), এই ভগ্নাংশটি আলোচনায় নিন। মনে করুন ফাংশনগুলোর দুটোই 0 হয়ে যাচ্ছে, যখন x – কে 0 ধরা হয়। তার মানে ƒ(0) = g (0) = 0. এবার মনে করুন উভয় ফাংশনকে অন্তরকলন করে পাওয়া গেল h(x) আর k(x), প্রথমটি ওপরে, দ্বিতীয়টি নিচে। এবার সেই একই কাজ করুনঃ x = 0 ব্যবহার করুন। তাতে যদি কাজ হয়, তার অর্থ একটা নির্দিষ্ট কিছু পাওয়া যায়—কোনো সসীম সংখ্যা বা অসীম সংখ্যা বা কোনো নির্দিষ্ট সংখ্যাই নয়, তাহলে তো সমস্যা চুকেই গেল। নইলে একই পদ্ধতি দ্বিতীয়বার চালিয়ে যান, যতবার লাগে ততবার।

এই করেই শেষ পর্যন্ত যুগযুগান্তরের সেই বিভীষিকাময় ঘৃণ্য বস্তুটির একটা সম্মানজনক আশ্রয় পাওয়া গেল। খেয়াল করুন যে লোপিতালের গাণিতিক দাওয়াইতে 0/0 কে এড়ানো তো হচ্ছেই না, বরং এটিকে রীতিমতো কাজে লাগানো হচ্ছে, যদিও আড়ালে কিন্তু সেই একই জিনিস—লিমিট। ক্যালকুলাসের এমন কোনো অংশ নেই যেখানে লিমিট পাবেন না আপনি। সুতরাং এটিকে এড়ানোর চেষ্টা না করে বরং পরিশ্রম করে শিখে ফেলাই ভালো, কী বলেন?