১৯৭০ সালের আগে আমার ব্যাপক অপেক্ষবাদ সম্পর্কীয় গবেষণার প্রধান বিষয়গুলি ছিল বৃহৎ বিস্ফোরণের অনন্যতা (big bang singularity) ঘটেছিল কিনা সেই প্রশ্ন নিয়ে। কিন্তু সেই বছর নভেম্বরে আমার মেয়ে লুসির জন্মের অল্পদিন পর এক বিকেলবেলা শুতে যাবার সময় আমি কৃষ্ণগহ্বর সম্পর্কে ভাবতে শুরু করি। অসুস্থতার দরুন আমার শুতে যেতে সময় লাগে সুতরাং আমি প্রচুর সময় পেয়েছিলাম। সেইস সময় স্থান-কালের কোন কোন বিন্দু কৃষ্ণগহ্বরের বাইরে এবং কোনগুলি ভিতরে এ সম্পর্কে সঠিক সংজ্ঞা ছিল না। কৃষ্ণগহ্বর এমন এক কেতা ঘটনা (set events) যেখান থেকে বেশি দূরে পলায়ন সম্ভব নয়- কৃষ্ণগহ্বরের এই রকম একটি সংজ্ঞার ধারণা নিয়ে এর আগেই আমি রজার পেনরোজের সঙ্গে আলোচনা করেছিলাম। বর্তমানে এই সংজ্ঞাই সাধারণভাবে গৃহীত হয়েছে। এর অর্থ হল কৃষ্ণগহ্বরের সীমানা অর্থাৎ ঘটনা দিগন্ত (event horizon) গঠিত হয় সেই সমস্ত আলোকরশ্মির পথরেখা ইয়ে যে রশ্মিগুলি কৃষ্ণগহ্বর থেকে নিষ্ক্রান্ত হতে পারে নি। সেগুলি অনন্তকাল ধরে সীমানায় ঘোরাফেরা করে (চিত্র- ৭.১)। ব্যাপারটা অনেকটা পুলিশের হাত থেকে পালানোর মতো, লোকটি পুলিশের হাত থেকে এক পা এগিয়ে আছে কিন্তু একেবারে পালিয়ে যেতে পারছে না।
হঠাত আমি বুঝতে পারলাম এই আলোকরশ্মিগুলির পথ কখনোই পরস্পরের অভিমুখে যেতে পারে না। যদি যায় তাহলে শেষ পর্যন্ত একটি অপরটির গায়ে গিয়ে পড়বে। এটা অনেকটা এমন লোকের সঙ্গে দেখা হওয়া যে পুলিশের কাছ থেকে পালাচ্ছে কিন্তু বিপরীত অভিমুখে- তোমরা দুজনেই ধরা পড়বে। (কিম্বা এক্ষেত্রে কৃষ্ণগহ্বরে পতিত হওয়া)। কিন্তু এই আলোকরশ্মিগুলিকে যদি কৃষ্ণগহ্বর গ্রাস করত তাহলে তারা কখনোই কৃষ্ণগহ্বরের সীমানায় যেতে পারত না। সুতরাং ঘটনা দিগন্তে আলোক রশ্মির গতিপথ হতে হোত সব সময়ই হয় সমান্তরাল, নয়তো পরস্পর থেকে দূরগামী। অন্য দৃষ্টিভঙ্গিতেও দেখা যায়, সেটা হলঃ ঘটনা দিগন্ত অর্থাৎ কৃষ্ণগহ্বরের সীমানা অনেকটা ছায়ার কিনারার মতো- ছায়াটি আসন্ন মৃত্যুর। সূর্যের মতো বহুদূরে অবস্থিত একটি উৎসের আলোকে যে ছাড়া পড়ে তার দিকে তাকালে আপনি দেখতে পাবেন কিনারার আলোকরশ্মিগুলি পরস্পর অভিমুখগামী নয়।
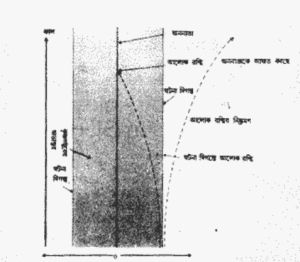
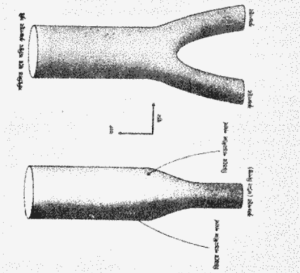
ঘটনা দিগন্ত থেকে নির্গত আলোকরশ্মিগুলি অর্থাৎ কৃষ্ণগহ্বরের সীমানা যদি কখনোই পরস্পরের অভিমুখী না হয় তাহলে ঘটনা দিগন্তের ক্ষেত্রের আয়তন (area) হয় একই থাকে নয়তো কালের সঙ্গে বৃদ্ধি পাবে কিন্তু কখনোই হ্রাস পাবে না। কারণ হ্রাস পাবার অর্থঃ সীমানার কিছু আলোকরশ্মিকে অন্তত পরস্পরের অভিমুখগামী হতে হবে। আসলে যখনই পদার্থ কিম্বা বিকিরণ কৃষ্ণগহ্বরে পতিত হবে তখনই তার ক্ষেত্রফল বৃদ্ধি পাবে (চিত্র- ৭.২), কিম্বা যদি দুটি কৃষ্ণগহ্বর পরস্পর সংঘর্ষের পর মিলিত হয়ে একটি কৃষ্ণগহ্বরে পরিণত হয় তাহলে অন্তিম কৃষ্ণগহ্বরের ঘটনা দিগন্তের ক্ষেত্রের আয়তন প্রথমের দুটী কৃষ্ণগহ্বরের ঘটনা দিগন্তের আয়তনের যোগফলের সমান হবে কিম্বা তার চাইতে বেশী হবে (চিত্র- ৭.৩)। ঘটনা দিগন্তের আয়তনের হ্রাসবৃদ্ধি না হওয়া ধর্মটি কৃষ্ণগহ্বরের সম্ভাব্য আচরণের একটি গুরুত্বপূর্ণ গণ্ডি বেঁধে দিল (important restriction)। আই আবিষ্কারে আমি এমনই উত্তেজিত হয়েছিলাম যে সে রাত্রে আমার ঘুম খুব বেশী হয়নি। পরের দিন আমি রজার পেনরোজকে টেলিফোন করি। তিনি আমার সঙ্গে একমত হন। আমার মনে হয় আসলে ক্ষেত্রের (area) এই ধর্ম তাঁর আগে থেকেই জানা ছিল। কিন্তু তিনি কৃষ্ণগহ্বরের সামান্য পৃথক একটি সংজ্ঞা ব্যবহার করেছিলেন। তিনি বুঝতে পারেন নি যে দুটি সংজ্ঞা অনুসারেই কৃষ্ণগহ্বরের সীমানা অভিন্ন হবে। সুতরাং তাঁর ক্ষেত্রফলও হবে অভিন্ন- অবশ্য যদি কৃষ্ণগহ্বরটি এমন অবস্থায় স্থিতিলাভ করে যে কালের সঙ্গে সে আর পরিবর্তিত হচ্ছে না।
কৃষ্ণগহ্বরের আয়তনের হ্রাস প্রাপ্তি না হওয়া এনট্রপি (entropy) নামক একটি ভৌতরাশিকে বিশেষভাবে মনে করিয়ে দেয়। এনট্রপি একটি তন্ত্রের (system) বিশৃঙ্খলার মাপ। সাধারণ অভিজ্ঞতায় দেখা যায় কোনো জিনিসকে নিজের উপর ছেড়ে দিলে তার ভিতর বিশৃঙ্খলা বৃদ্ধির প্রবণতা বাড়ে। (বাড়ির মেরামত বন্ধ করে দিলেই সেটা বোঝা যায়) আমরা বিশৃঙ্খলা থেকে শৃঙ্খলা সৃষ্টি করতে পারি (উদাহরণঃ বাড়িটা রং করা যেতে পারে) কিন্তু এই জন্য প্রয়োজন চেষ্টা করা কিম্বা শক্তি ব্যয় করা। ফলে প্রাপ্তরা সুশৃঙ্খল শক্তির পরিমাণ হ্রাস পায়।
এ চিন্তনে যথাযথ বিবরণের নাম তাপগতিবিদ্যার দ্বিতীয় বিধি (second law of thermodynamics)। এই বিধি অনুসারে একটি বিচ্ছিন্নতন্ত্রের এনট্রপি সর্বদা বৃদ্ধি পায়। যখন দুটি তন্ত্র সংযুক্ত হয় তখন সংযুক্ত তন্ত্রের এনট্রপি একক দুটি তন্ত্রের এনট্রপির যোগফলের চাইতে বেশি। উদাহরণঃ একটি বাক্সের ভিতরকার বায়বীয় পদার্থ- অণুতন্ত্রের (system of gas molecules) কথা বিচার করুন। অণুগুলিকে ছোট ছোট বিলিয়ার্ড বলের মতো ভাবা যেতে পারে। সেগুলির অবিচ্ছিন্নভাবে পরস্পরের সঙ্গে সংঘর্ষ হচ্ছে এবং বাক্সের দেওয়ালে ঠোক্কর খেয়ে ফিরে আসছে। বায়বীয় পদার্থের তাপমাত্রা যত বাড়বে, অণুগুলিও তত দ্রুত চলমান হবে। বাক্সের দেওয়ালের সঙ্গে সংঘর্ষও হবে কঠিনতর এবং তত বেশি ঘন ঘন আর দেওয়ালের উপর তাদের প্রদত্ত বহির্মুখী চাপও বৃদ্ধি পাবে। অনুমান করা যাক শুরুতে সবটা অণুই বাক্সের বাঁদিকে আবদ্ধ রয়েছে এবং সে দিকটা একটি পার্টিশন (partition- বিভাজক দেওয়াল) দিয়ে পৃথক করা। পার্টিশনটা সরিয়ে নিলে অণুগুলি ছড়িয়ে পড়তে চাইবে এবং বাক্সের দুটি অংশই দখন করে নেবে। কোনো এক পরবর্তী সময়ে আপতনের ফলে (by chance) সবকটি অণুই ডানদিকের অর্ধাংশে থাকতে পারে কিম্বা বাম দিকের অর্ধাংশে ফিরে যেতে পারে কিন্তু সর্বাধিক সম্ভাবনা দুটি দিকেই মোটামুটি একই সংখ্যক অণু থাকবে। প্রাথমিক অবস্থায় যখন সমস্ত অণুই বাম দিকে ছিল তার তুলনায় এই ধরণের অবস্থায় শৃঙ্খলা কম- অর্থাৎ বিশৃঙ্খলা বেশি। সুতরাং বলা যায় বায়বীয় পদার্থের এনট্রপি বেড়েছে। অনুরূপভাবে অনুমান করা যাকঃ শুরু করা হয়েছে দুটি বাক্স নিয়ে- একটিতে রয়েছে অক্সিজেন অণু, অন্যটিতে নাইট্রোজেন অণু। দুটি বাক্স জুড়ে যদি মাঝখানের দেওয়ালটি সরিয়ে নেওয়া যায় তাহলে অক্সিজেন আর নাইট্রোজেন অণু মিশতে শুরু করবে। পরবর্তীকালে যে অবস্থার সম্ভাবনা সব চাইতে বেশি সেই অবস্থায় দুটি বাক্সের সর্বত্রই অক্সিজেন ও নাইট্রোজেন অণুগুলি প্রায় সমানভাবে মিশ্রিত থাকবে। এই অবস্থায় প্রথমাবস্থার দুটি বাক্সের তুলনায় শৃঙ্খলা থাকবে কম, সুতরাং এনট্রপি থাকবে বেশি।
নিউটনের মহাকর্ষীয় বিধির মতো বিজ্ঞানের অন্যান্য বিধির তুলনায় তাপগতিবিদ্যার দ্বিতীয় বিধির স্থান একটু অন্যরকম। তপগতিবিদ্যার দ্বিতীয় বিধি বিরাট সংখ্যাগুরু ক্ষেত্রে সত্য- কিন্তু সর্বক্ষেত্রে সত্য নয়। প্রথম বাক্সটির সমস্ত বায়বীয় পদার্থের অণু পরবর্তীকালে অর্ধেক বাক্সে পাওয়ার সম্ভাবনা বহু কোটি বারের ভিতর একবার। তবে এরকম ঘটনা ঘটা সম্ভব। কিন্তু কাছাকাছি একটি কৃষ্ণগহ্বর থাকলে দ্বিতীয় বিধি অমান্য করার একটি সহজতর পথ আছে বলে মনে হয়। বায়বীয় পদার্থের বাক্সে যেরকম ছিল সেইরকম প্রচুর এনট্রপিসম্পন্ন খানিকটা পদার্থ কৃষ্ণগহ্বরে ফেলে দিন। কৃষ্ণগহ্বরের বাইরে অবস্থিত পদার্থের মোট এনট্রপি হ্রাস পাবে। তবুও অবশ্য বলা যেতে পারে কৃষ্ণগহ্বরের অভ্যন্তরের এনট্রপি সমেত মোট এনট্রপি হ্রাস পায়নি। কিন্তু কৃষ্ণগহ্বরের ভিতরটা দেখা আমাদের পক্ষে সম্ভব নয়, সেইজন্য অভ্যন্তরস্থ পদার্থে কতটা এনট্রপি আছে সেটা আমরা বুঝতে পারব না। খুব ভাল হত যদি কৃষ্ণগহ্বরের এমন কোনো অবয়ব থাকত যার সাহায্যে কৃষ্ণগহ্বরের বাইরের পর্যবেক্ষক কৃষ্ণগহ্বরের এনট্রপি বলতে পারত এবং যখনই পদার্থ এনট্রপি বহন করে কৃষ্ণগহ্বরে পড়ত, ঐ অবয়বও তখন বাড়ত। যখনই কৃষ্ণগহ্বরের ভিতর পদার্থ পতিত হয় তখনই ঘটনা দিগন্তের ক্ষেত্রফল (area) বৃদ্ধি পায়- উপরে লিখিত এই আবিষ্কারের পর জেকব বেকেনস্টাইন (Jacob Bekenstein) নামে প্রিন্সটনের একজন গবেষণাকারী ছাত্র প্রস্তাবনা করেন, ঘটনা দিগন্তের ক্ষেত্রফল কৃষ্ণগহ্বরের এনট্রপির একটি মাপ। এনট্রপি বহনকারী পদার্থ যেমন যেমন কৃষ্ণগহ্বরে পতিত হয়, ঘটনা দিগন্তের ক্ষেত্রফলও তেমন বৃদ্ধি পায়। সুতরাং কৃষ্ণগহ্বরের বাইরের পদার্থ এবং ঘটনাদিগন্তের ক্ষেত্রফলের যোগফল কখনোই হ্রাস পায় না।
মনে হয়েছিল এই প্রস্তাবনা (suggestion) অধিকাংশ পরিস্থিতিতেই তাপগতিবিদ্যার দ্বিতীয় বিধি লঙ্ঘন করাকে বাধা দেবে। কিন্তু একটি মারাত্মক দোষ থেকে গিয়েছিল। কৃষ্ণগহ্বরের যদি এনট্রপি থাকে তাহলে তার উষ্ণতাও থাকা উচিত। কিন্তু যে কোনো বস্তু একটি বিশেষ তাপমাত্রায় একটি বিশেষ হারে বিকিরণ করবে। সাধারণ অভিজ্ঞতায় দেখা যায় আগুনে একটি লৌহদন্ড গরম করলে লৌহদন্ডটি লাল হয় এবং তা থেকে বিকিরণ নির্গত হতে থাকে। কিন্তু উষ্ণতা কম হলেও বস্তুপিন্ড থেকে বিকিরণ হয়। সাধারণ অবস্থায় সেটা নজরে পড়ে না কারণ পরিমাণটা খুবই কম। দ্বিতীয় বিধি ভঙ্গ করা বন্ধ করার জন্যই এই বিকিরণ প্রয়োজন। সুতরাং কৃষ্ণগহ্বর থেকে বিকিরণ নির্গত হওয়া উচিত কিন্তু সংজ্ঞা অনুসারে কৃষ্ণগহ্বরগুলি এমন বস্তু যা থেকে কোনো কিছু নির্গত হওয়া সম্ভব নয়। সুতরাং মনে হয়েছিল একটি কৃষ্ণগহ্বরের ঘটনা দিগন্তের ক্ষেত্রফলকে তার এনট্রপি বলে বিচার করা ঠিক নয়। ১৯৭২ সালে আমি, ব্রান্ডন কার্টার (Brandon Carter) এবং জিম বার্ডিন (Jim Bardeen) নামে একজন আমেরিকান সহকর্মীর সঙ্গে একটি প্রবন্ধ লিখি। সেই প্রবন্ধে আমরা দেখিয়েছিলাম এনট্রপি এবং ঘটনা দিগন্তের ক্ষেত্রফলের ভিতরে যথেষ্ট সাদৃশ্য থাকা সত্ত্বেও এই আপাতদৃষ্ট সর্বনাশা সঙ্কট (fatal Difficulty) রয়েছে। এ কথাটা আমার স্বীকার করা অবশ্যই উচিৎঃ এই প্রবন্ধ লেখার আংশিক কারণ ছিল বেকেনস্টাইন (Bekenstein) সম্পর্কে আমার বিরক্তি। আমার মনে হয়েছিল ঘটনা দিগন্তের ক্ষেত্রফল সম্পর্কে আমার আবিষ্কারের তিনি অপব্যবহার করেছেন। শেষ পর্যন্ত কিন্তু দেখা গেল তিনি ছিলেন মূলত সঠিক তবে সঠিক এমনভাবে যা তিনি নিশ্চয়ই আশা করেন নি।
১৯৭৩ সালের সেপ্টেম্বর মাসে আমি মস্কো পরিদর্শনে যাই। সেই সময় আমি ইয়াকভ জেল্ডোভিচ (Yakov Zeldovich) এবং আলেকজান্ডার স্টারোবিনস্কি (Alexander Starobinsky) নামে দুই প্রধান সোভিয়েট বিশেষজ্ঞের সঙ্গে কৃষ্ণগহ্বর সম্পর্কে আলোচনা করি। তাঁরা আমাকে বোঝালেন কোয়ান্টাম বলবিদ্যার অনিশ্চয়তার নীতি অনুসারে ঘূর্ণায়মান কৃষ্ণগহ্বরগুলি কণিকা সৃষ্টি করবে এবং বিকিরণ করবে। তাঁদের ভৌত যুক্তিভিত্তিক মত আমি মেনে নিয়েছিলাম কিন্তু তাঁদের বিকিরণ গণনার গাণিতিক পদ্ধতি আমার পছন্দ হয়নি। সুতরাং আমি একটি উন্নততর গাণিতিক পদ্ধতি আবিষ্কারের চেষ্টা শুরু করলাম। ১৯৭৩ সালের নভেম্বর মাসে অক্সফোর্ড একটি বেসরকারী সেমিনারে (শিক্ষাকেন্দ্রে আলোচনা সভা- seminar) আমি সেই পদ্ধতির বিবরণ দান করি। সে সময় কতটা বিকিরণ হবে সেটা আমি গণনা করে নির্ধারণ করিনি। আমার আশা ছিল জেল্ডোভিচ এবং স্টারোবিনস্কির পূর্বাভাস অনুসারে ঘূর্ণায়মান কৃষ্ণগহ্বর থেকে যে বিকিরণ হয় শুধুমাত্র সেটাই আবিষ্কার করা। কিন্তু গণনার পর আমি বিরক্তি আর বিস্ময়ের সঙ্গে দেখলাম এমনকি অঘূর্ণায়মান কৃষ্ণগহ্বরগুলিও আপাতদৃষ্টিতে কণিকা সৃষ্টি করতে পারে এবং স্থির হারে বিকিরণ করতে পারে। প্রথমে আমি ভেবেছিলাম এই বিকিরণের নির্দেশ হল আমার ব্যবহৃত একটি আসন্নতা (approximation) সিদ্ধ নয় )not valid)। আমার ভয় ছিল বেকেনস্টাইন ব্যাপারটা জানলে এটাকেই কৃষ্ণগহ্বরের এনট্রপি সম্পর্কে তাঁর নিজস্ব চিন্তাধারার সপক্ষে যুক্তি হিসাবে ব্যবহার করবেন, এ ব্যাপারটি আমার তখনও পছন্দ ছিল না। কিন্তু আমি যতই ভেবেছি ততই আমার মনে হয়েছে আসন্নতাগুলি প্রকৃতই সিদ্ধ হওয়া উচিত (ought to hold)। নির্গত কণিকাগুলির বর্ণালী একটি উত্তপ্ত বস্তুপিন্ডের যে বর্ণালী হওয়া উচিত তার সঙ্গে অভিন্ন এবং কৃষ্ণগহ্বর থেকে কণিকা নির্গমনের হার এমন যে সে হার নির্ভুলভাবে দ্বিতীয় বিধি ভঙ্গ হওয়া প্রতিরোধ করে। নির্গমন যে বাস্তব সে সম্পর্কে উপরোক্ত তথ্যগুলিই শেষ পর্যন্ত আমার বিশ্বাস উৎপাদন করে। তারপর থেকে অন্য অনেকে নানাভাবে এই গণনার পুনবৃত্তি (repeated) করেছেন। উষ্ণতা (temperature) যুক্ত একটি উত্তপ্ত বস্তুপিন্ডেরই মতো কৃষ্ণগহ্বর থেকে কণিকা নির্গত হওয়া উচিৎ এবং সেটা থেকে বিকিরণও হওয়া উচিৎ। এই তাপমাত্রা (temperature) নির্ভর করবে শুধুমাত্র কৃষ্ণগহ্বরটির ভরের উপরঃ ভর যত বেশী হবে তাপমাত্রা হবে তত কম। উপরে উল্লিখিত প্রতিটি গণনাতেই এই তথ্য সমর্থিত হয়েছে।
আমরা জানি কৃষ্ণগহ্বরের ঘটনা দিগন্ত থেকে কোনো কিছুই নির্গত হতে পারে না, তাহলে কৃষ্ণগহ্বর থেকে কণিকা নির্গত হওয়া কি করে সম্ভব? উত্তরটি দিচ্ছে কোয়ান্টাম তত্ত্বঃ কণিকাগুলি কৃষ্ণগহ্বরের ভিতর থেকে আসে না, আসে কৃষ্ণগহ্বরের ঘটনাদিগন্তের ঠিক বাইরে “শূন্য” (empty) স্থান থেকে। এটা আমরা বুঝতে পারি নিম্নলিখিত উপায়েঃ আমরা যাকে শূন্যস্থান বলে ভাবি সেটা সম্পূর্ণ শূন্য হতে পারে না, কারণ তা যদি হয় তাহলে মহাকর্ষীয় ক্ষেত্র, বিদ্যুৎ চুম্বকীয় ক্ষেত্রের মতো সমস্ত ক্ষেত্রকেই নির্ভুলভাবে শূন্য হতে হবে। কিন্তু একটি ক্ষেত্রের মান (value) এবং কালের সঙ্গে তার পরিবর্তনের হার প্রায় একটি কণিকার অবস্থান এবং গতিবেগের মতোঃ অনিশ্চয়তার নীতি (uncertainly principle) নিহিতার্থ অনুসারে এই সমস্ত রাশিগুলির একটিকে যত নিখুঁতভাবে জানা যায় অপরটি সম্পর্কে জ্ঞান ততই কম নিখুঁত হয়। সুতরাং শূন্যস্থানে ক্ষেত্রকে ঠিক নিখুঁতভাবে শূন্য বলে স্থির করা যায় না। কারণ, তাহলে এর একটি নিখুঁত মান (শূন্য) এবং পরিবর্তনের নিখুঁত হার (এ ক্ষেত্রেও শূন্য) এই দুটিই থেকে যাবে। ক্ষেত্রের (field) মানের (value) একটি সর্বনিম্ন মানের অনিশ্চয়তা অর্থাৎ কোয়ান্টাম হ্রাসবৃদ্ধি (quantum fluctuation) থাকতেই হবে। এই হ্রাসবৃদ্ধিকে মহাকর্ষ কণিকা কিম্বা আলোক কণিকার জোড় হিসাবে ভাবা যেতে পারে- এরা কোনো সময়ে একসঙ্গে দেখা দেয়, আলাদা হয়ে যায়, আবার একত্র হয় এবং পরস্পরকে বিনাশ করে। সূর্যের মহাকর্ষীয় বল যারা বহন করে এগুলিও সেগুলির মতো কল্পিত (virtual) কণিকা। বাস্তব কণিকাগুলিকে যেরকম কণিকা অভিজ্ঞাপক যন্ত্র (particle detector) দিয়ে প্রত্যক্ষভাবে পর্যবেক্ষণ করা যায়, এগুলিকে সেরকম পর্যবেক্ষণ করা যায় না। পরমাণুর ভিতরকার ইলেক্ট্রনের কক্ষের পরিবর্তনে শক্তির যে সামান্য পরিবর্তন হয় তাই দিয়ে কিন্তু এগুলির পরোক্ষ ক্রিয়া মাপা যায় এবং এর সঙ্গে তাত্ত্বিক ভবিষ্যদ্বাণীর উল্লেখযোগ্য পরিমাণে মিল রয়েছে। অনিশ্চয়তার নীতির আর একটি ভবিষ্যদ্বাণী হলঃ পদার্থ কণিকার সমরূপ কল্পিত (virtual pair) জোড় আরো দেখা যাবে, যেমন ইলেক্ট্রন কিম্বা কার্কের (quark) জোড়। এক্ষেত্রে কিন্তু জোড়ের একটি হবে কণিকা এবং অপরটি হবে বিপরীত কণিকা (আলোক এবং মহাকর্ষের বিপরীত কণিকা এবং কণিকা অভিন্ন)।
যেহেতু শূন্যতা থেকে শক্তি সৃষ্টি হতে পারে না সেইজন্য কণিকা/বিপরীত কণিকার জোড়ের একটি অংশীদারের থাকবে পরা (positive) শক্তি অপর অংশীদারের থাকবে অপরা (negative) শক্তি। অপরা শক্তিসম্পন্ন কণিকা অভিশপ্ত স্বল্পায়ু কল্পিত কণিকা, কারণ বাস্তব কণিকাগুলি স্বাভাবিক অবস্থায় সব সময় পরা শক্তিসম্পন্ন হয়। একে সেইজন্য অবশ্যই নিজের অংশীদার খুঁজে বার করে তার সঙ্গে বিনষ্ট হতে হবে। তবে বৃহৎ ভরসম্পন্ন একটি বস্তুপিন্ডের নিকটবর্তী কণিকার শক্তি সেই বস্তুপিন্ড থেকে দূরবর্তী অবস্থার তুলনায় কম হবে। তার কারণ, বস্তুপিন্ডটির মহাকর্ষীয় আকর্ষণ থেকে কণিকাটিকে দূরে নিয়ে যেতে শক্তি তখনো প্রয়োজন হবে। স্বাভাবিক অবস্থায় কণিকার শক্তি হবে পরা (positive), কিন্তু একটি কৃষ্ণগহ্বরের ভিতরকার মহাকর্ষীয় ক্ষেত্র এত বেশি শক্তিশালী যে, সেখানে বাস্তব কণিকাগুলিরও অপরা শক্তি (negative) থাকতে পারে। কৃষ্ণগহ্বরের অস্তিত্ব থাকলে অপরা শক্তিসম্পন্ন কল্পিত কণিকার কৃষ্ণগহ্বরে পতিত হয়ে বাস্তব কণিকা কিম্বা বিপরীত কণিকায় পরিণত হওয়া সম্ভব। এক্ষেত্রে তাকে আর অংশীদারের সঙ্গে বিনষ্ট হবে হবে না। এর পরিত্যক্ত অংশীদারও কৃষ্ণগহ্বরে পতিত হতে পারে। কিম্বা পরাশক্তি থাকার ফলে বাস্তব কণিকা কিম্বা বিপরীত কণিকারূপে কৃষ্ণগহ্বরের নিকট থেকে অপসারণও করতে পারে (চিত্র – ৭.৪)। দূরস্থিত একজন পর্যবেক্ষকের মনে হবে এগুলি কৃষ্ণগহ্বর থেকে নির্গত হয়েছে। কৃষ্ণগহ্বরটি যত ছোট হবে, অপরা শক্তিসম্পন্ন একটি কণিকার বাস্তব কণিকায় রূপান্তরিত হওয়ার আগে তত কম দূরত্ব অতিক্রম করতে হবে। সুতরাং নির্গত হওয়ার হারও তত বেশি হবে এবং কৃষ্ণগহ্বরের আপাতদৃষ্ট তাপমাত্রাও তত বেশী হবে।
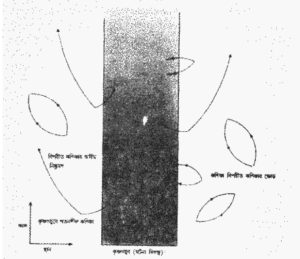
বহির্গামী বিকিরণের পরা শক্তির সঙ্গে সমতা রক্ষা করবে কৃষ্ণগহ্বরের অপরা শক্তিসম্পন্ন কণিকাগুলির স্রোত। আইনস্টাইনের সমীকরণ E = mc2 অনুসারে (E- শক্তি, m- ভর এবং c- আলোকের দ্রুতি) শক্তি ভরের সমানুপাতিক (proportional), সুতরাং কৃষ্ণগহ্বরের অন্তর্গামী অপরা শক্তির স্রোত তার ভর কমিয়ে দেবে। কৃষ্ণগহ্বরের ভর কমলে তার ঘটনাদিগন্তের ক্ষেত্রফলও (area) ক্ষুদ্রতর হয়। কিন্তু কৃষ্ণগহ্বরের এনট্রপির এই হ্রাসপ্রাপ্তির ক্ষতিপূরণ হতে পারে নির্গত বিকিরণের এনট্রপি দ্বারা, এমন কি, তার চাইতেও বেশি হতে পারে। সুতরাং দ্বিতীয় বিধি কখনো লঙ্ঘিত হয় না।
তাছাড়া কৃষ্ণগহ্বরের ভর যত কম হয় তার তাপমাত্রা তত বেশি হয়। সুতরাং কৃষ্ণগহ্বরের ভর হ্রাস পেলে তার তাপমাত্রা বৃদ্ধি পাবে, বৃদ্ধি পাবে সেটা থেকে নির্গত হওয়ার (emission) হার- অতএব তার ভর আরও দ্রুত হ্রাস পাবে। কৃষ্ণগহ্বরের ভর যখন শেষ পর্যন্ত অত্যন্ত অল্প হয়ে যায় তখন ব্যাপারটা কি দাঁড়ায় সেটা খুব স্পষ্ট নয়, কিন্তু সবচাইতে যুক্তিসঙ্গত অনুমান হলঃ অন্তিমে নির্গত হওয়ার এক বিরাট বিস্ফোরণের ফলে কৃষ্ণগহ্বরটি সম্পূর্ণ মিলিয়ে যাবে। এই বিস্ফোরণটি হতে পারে বহু মিলিয়ন হাইড্রোজেন বোমার সমান।
সূর্য থেকে কয়েকগুণ বেশি ভরসম্পন্ন একটি কৃষ্ণগহ্বরের তাপমাত্রা হবে চরম শূন্য (absolute zero) থেকে এক ডিগ্রীর এক কোটি ভাগের এক ভাগ বেশি। যে মাইক্রোওয়েভ বিকিরণ (microwave radiation) সমগ্র মহাবিশ্বে ব্যাপ্ত তার তাপমাত্রা (চরম শূন্য থেকে প্রায় ২.৭ ডিগ্রী বেশী) থেকে এই তাপমাত্রা অনেক কম। সুতরাং এই সমস্ত কৃষ্ণগহ্বর যা বিশোষণ করে তার তুলনায় তা থেকে নির্গত হবে (emit) অনেক কম। অনন্তকাল ধরে সম্প্রসারিত হওয়াই যদি মহাবিশ্বের নিয়তি হয় তাহলে এক সময় মাইক্রোওয়েভ বিকিরণের তাপমাত্রা এই ধরনের কৃষ্ণগহ্বরের তাপমাত্রার চাইতে কমে যাবে। সুতরাং কৃষ্ণগহ্বরটি ক্রমশ ভর পরিত্যাগ করতে থাকবে। কিন্তু তবুও এর তাপমাত্রা এত কম হবে যে কৃষ্ণগহ্বরটি উবে যেতে প্রায় মিলিয়ন মিলিয়ন মিলিয়ন মিলিয়ন মিলিয়ন মিলিয়ন মিলিয়ন মিলিয়ন মিলিয়ন মিলিয়ন মিলিয়ন (একের পিঠে ছেষট্টিটি শূন্য) বৎসর লাগবে। এই কাল মহাবিশ্বের বয়সের চাইতে অনেক বেশি। মহাবিশ্বের বয়স মাত্র দশ থেকে কুড়ি হাজার মিলিয়ন বৎসর (এক কিম্বা দু-এর পিঠে দশটা শূন্য)। এদিকে আবার একাধিক আদিম কৃষ্ণগহ্বর থাকতে পারে। সেগুলির ভরও হতে পারে অনেক কম। এগুলি উৎপন্ন হওয়ার কারণ ছিল মহাবিশ্বের অতি আদিম অবস্থায় যে সমস্ত অংশের সুষম অংশের বিকাশের সঙ্গে অসঙ্গতি ছিল, সেগুলির চুপসে যাওয়া। ষষ্ঠ পরিচ্ছেদে ে তথ্য উল্লেখ করা হয়েছে। এই রকম কৃষ্ণগহ্বরের তাপমাত্রা অনেক বেশি হবে আর সেগুলি থেকে বিকিরণ নির্গত হওয়ার হারও হবে অনেক বেশি। আদিম একটি কৃষ্ণগহ্বরের (primordial black hole) শুরুতে যদি ভর থাকে একশ কোটি টন তাহলে তার আয়ু হবে মোটামুটি আমাদের মহাবিশ্বের আয়ুর সমান। যে সমস্ত আদিম কৃষ্ণগহ্বরের প্রাথমিক ভর এর চাইতে কম ছিল সেগুলি ইতিপূর্বে সম্পূর্ণ উবে গিয়েছে (completely evaporated), কিন্তু যেগুলির ভর এর চাইতে সামান্য বেশি ছিল সেগুলি থেকে এখনো এক্স-রে এবং গামা-রে (X-Ray & Gamma Ray) রূপে বিকিরণ নির্গত হচ্ছে। এই এক্স-রে এবং গামা-রে গুলি আলোক তরঙ্গের মতো কিন্তু সেগুলির তরঙ্গদৈর্ঘ্য অনেক কম। এই গহ্বরগুলির কৃষ্ণ বিশেষণের বিশেষ কোনো অর্থ নেই। এগুলি আসলে উত্তপ্ত হয়ে শ্বেতবর্ণ ধারণ করে এবং এগুলি থেকে দশ হাজার মেগাওয়াট হারে শক্তি নির্গত হয়।
এইরকম একটি কৃষ্ণগহ্বর দশটি বৃহৎ বিদ্যুৎ কেন্দ্রে চালাতে পারে- অবশ্য যদি তার শক্তিকে এই কাজে ব্যবহার করা সম্ভব হয়। ব্যাপারটা একটু শক্ত হবে- পর্বতপ্রমান একটি কৃষ্ণগহ্বর সংকুচিত (compresses) হয়ে এক ইঞ্চির এক মিলিয়ন ভাগের এক মিলিয়ন ভাগ হয়ে যাবে অর্থাৎ তার আকার হবে একটি পরমাণুর কেন্দ্রকের সমান! এরকম একটি কেন্দ্রক যদি ভূপৃষ্ঠে থাকে তাহলে সেটা পৃষ্ঠ ভেদ করে পৃথিবীর কেন্দ্রে পৌঁছে যাবে। তাকে বাধা দেওয়ার কোনো উপায় থাকবে না। এটা পৃথিবীর ভিতর দিয়ে দোলকের মতো যাতায়াত করতে থাকবে এবং শেষ পর্যন্ত পৃথিবীর কেন্দ্রে গিয়ে স্থিতিলাভ করবে। সুতরাং এ থেকে নির্গত শক্তি ব্যবহার করা যাবে, একে স্থাপন করার সেরকম স্থান হতে পারে শুধু এটাকে পৃথিবীকে প্রদক্ষিণ করছে এরকম কোনো কক্ষপথে স্থাপন করলে। এটাকে পৃথিবীকে প্রদক্ষিণ করার মতো কক্ষপথে স্থাপন করার একমাত্র উপায় একটি বিরাট ভরসম্পন্ন বস্তুপিন্ডকে টেনে এনে এর সামনে স্থাপন করা। ব্যাপারটা অনেকটা গাধার সামনে গাজর রাখার মতো। প্রস্তাবটা খুব বাস্তব বলে মনে হয় না অন্তত নিকট ভবিষ্যতে তো নিশ্চয়ই নয়।
কিন্তু যদি এই আদিম কৃষ্ণগহ্বরগুলি থেকে নির্গত শক্তিকে ব্যবহার করা সম্ভব নাও হয় তাহলে এগুলি পর্যবেক্ষণ করার সম্ভাবনা কতটা? এই আদিম কৃষ্ণগহ্বরগুলি থেকে তাদের জীবনকালের অধিকাংশ সময় যে গামা নির্গত হয় আমরা সেই রশ্মি খুঁজতে পারি। এই কৃষ্ণগহ্বরগুলি বহুদূরে অবস্থিত, সুতরাং অধিকাংশ কৃষ্ণগহ্বর থেকে বিকিরণ হবে অত্যন্ত দুর্বল।
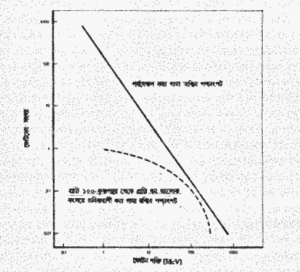
কিন্তু সবগুলি একত্র হলে হয়তো সনাক্ত করাও যেতে পারে। গামা রশ্মির এরকম একটি পশ্চাৎপট আমরা সত্যিই দেখতে পাই। চিত্র- ৭.৫ থেকে দেখা যায় পর্যবেক্ষণ করা তীব্রতার বিভিন্ন স্পন্দাংকে (frequency- প্রতি সেকেন্ডে তরঙ্গের সংখ্যা) কি রকম পার্থক্য হয়। কিন্তু এই পশ্চাৎপট আদিম কৃষ্ণগহ্বর ছাড়া অন্য কোনোভাবেও সৃষ্টি হয়ে থাকতে পারে- হয়তো হয়েছেও তাই। চিত্র- ৭.৫ –এ বিন্দুরেখা দিয়ে দেখানো হয়েছে, যদি ঘন আলোকবৎসরে (cubic light year) গড়ে তিনশ থাকে তাহলে কিভাবে আদিম কৃষ্ণগহ্বর থেকে নির্গত গামা রশ্মির স্পন্দাংক অনুসারে তীব্রতা পরিবর্তিত হয়। সুতরাং বলা যেতে পারে গামা রশ্মির পশ্চাৎপট পর্যবেক্ষণ করে কৃষ্ণগহ্বরের সপক্ষে কোনো ইতিবাচক সাক্ষ্য (positive evidence) পাওয়া যায় না। কিন্তু তা থেকে এ সংবাদ আমরা পাই যে মহাবিশ্বের প্রতি ঘন আলোকবৎসরে এর সংখ্যা গড়ে তিনশ’- এর বেশি হতে পারে না। এই সীমার অর্থ হলঃ আদিম কৃষ্ণগহ্বরের ভর মহাবিশ্বের মোট পদার্থের দশ লক্ষ ভাগের এক ভাগের বেশী হবে না।
আদিম কৃষ্ণগহ্বরগুলি এত বিরল হওয়ার ফলে মনে হতে পারে- আমরা গামা রশ্মির একক উৎস হিসাবে পর্যবেক্ষণ করতে পারি- আমাদের এত নিকটে কোনো কৃষ্ণগহ্বর পাওয়ার সম্ভাবনা কম। কিন্তু মহাকর্ষ কৃষ্ণগহ্বরগুলিকে যে কোনো পদার্থের দিকে আকর্ষণ করবে, সুতরাং নীহারিকার ভিতরে এবং তার কাছাকাছি কৃষ্ণগহ্বরগুলির অনেক বেশি সংখ্যায় থাকা উচিৎ। যদিও গামা রশ্মির পশ্চাৎপট থেকে আমরা জানতে পারি প্রতি ঘন আলোকবর্ষে গড়ে তিনশ’র বেশি কৃষ্ণগহ্বর থাকতে পারে না তবুও আমাদের নিজেদের নীহারিকায় এগুলির সংখ্যা কি রকম হতে পারে সে সম্পর্কে আমরা কিছুই জানতে পারি না। এদের সংখ্যা যদি এর চাইতে দশ লক্ষ গুণ বেশি হোত তাহলে আমাদের নিকটতম কৃষ্ণগহ্বর হয়তো প্রায় একশ কোটি কিলোমিটার দূরে অবস্থিত হোত- অর্থাৎ আমাদের জানা দূরতম গ্রহ প্লুটোর কাছাকাছি হোত। এই দূরত্বে থাকলেও একটি কৃষ্ণগহ্বর থেকে অবিচ্ছিন্ন বিকিরণ সনাক্ত করা কঠিন হোত- এমনকি সেই বিকিরণ দশ হাজার মেগাওয়াট হলেও। একটি আদিম কৃষ্ণগহ্বর পর্যবেক্ষণ করতে হলে একটি যুক্তিসঙ্গত সময়ের ভিতরে (ধরা যাক এক সপ্তাহ) একই অভিমুখ থেকে আগমনশীল কয়েকটি গামা রশ্মির কোয়ান্টা সনাক্ত করতে হবে। তা না হলে সেগুলি শুধুমাত্র পশ্চাৎপটের অংশমাত্র হতে পারে। কিন্তু প্ল্যাঙ্কের (Planck) কোয়ান্টাম নীতি আমাদের বলছে প্রতিটি গামা রশ্মির কোয়ান্টাম অতিশয় উচ্চশক্তিসম্পন্ন তার কারণ গামা রশ্মিগুলির স্পন্দাংক খুবই বেশি। সুতরাং এমনকি দশ হাজার মেগাওয়াট বিকিরণ করতেও খুব বেশি কোয়ান্টা প্রয়োজন হবে না। প্লুটোর দূরত্ব থেকে আগমনশীল কয়েকটি কোয়ান্টা পর্যবেক্ষণ করতে এত বড় গামা রশ্মি অভিজ্ঞাপক যন্ত্র (detector) দরকার যা এখনো তৈরি হয়নি। তাছাড়া যন্ত্রটিকে থাকতে হবে স্থানে (space), কারণ, গামা রশ্মি আবহমণ্ডল (atmosphere) ভেদ করতে পারে না।
অবশ্য প্লুটোর দূরত্বের মতো নিকটবর্তী একটি কৃষ্ণগহ্বর যদি তার জীবনকালের শেষ প্রান্তে এসে বিস্ফোরিত হয় তাহলে তার অন্তিম বিকিরণ সনাক্ত করা সহজ হবে। কিন্তু কৃষ্ণগহ্বরটি যদি গত এক হাজার কিম্বা দু’হাজার কোটি বছর বিকিরণ করে থাকে তাহলে তার অন্তিম সময় কয়েক মিলিয়ন বছর আগে পরে না হয়ে আগামী কয়েক বছরের ভিতর হওয়ার সম্ভাবনা একটু কম। সুতরাং আপনার গবেষনার জন্য বরাদ্দ টাকা ফুরিয়ে যাওয়ার আগে এরকম একটি বিস্ফোরণ দেখবার একটি যুক্তিপূরণ সম্ভাবনা চাইলে প্রায় এক আলোকবর্ষ দূরত্বের ভিতরে যে কোন বিস্ফোরণ সনাক্ত করার উপায় বার করতে হবে। তারপরেও আপনার সমস্যা থাকবেঃ বিস্ফোরণ থেকে নির্গত কয়েকটি গামা রশ্মি কোয়ান্টা ধরা পড়বার মতো একটি বৃহৎ গামা রশ্মি অভিজ্ঞাপক যন্ত্র। তবে এক্ষেত্রে সবকটি কোয়ান্টা যে একই অভিমুখ থেকে আসছে সেটা নির্ধারণ করার প্রয়োজন হবে না। সবকটি কোয়ান্টা অতি অল্পকালের ব্যবধানে পৌঁছেছে- এটা পর্যবেক্ষণ করতে পারলেই মোটামুটি নিশ্চিত হওয়া যাবে যে ওরা সবকটি একই বিস্ফোরণ থেকে এসেছে।
আমি কৃষ্ণগহ্বরের নির্দেশ দিতে পারে এরকম একটি অভিজ্ঞাপক যন্ত্র (detector) হল পৃথিবীর সম্পূর্ণ আবহমণ্ডল (যাই হোক না কেন, এর চাইতে বড় অভিজ্ঞাপক যন্ত্র নির্মাণের সম্ভাবনা আমাদের খুবই কম)। একটি উচ্চশক্তি সম্পন্ন গামা রশ্মি কোয়ান্টাম একটি পরমাণুকে আঘাত করলে সেটা ভেঙ্গে জোড়ায় জোড়ায় ইলেক্ট্রন আর পজিট্রন (বিপরীত ইলেক্ট্রন) সৃষ্টি করে। এগুলি পরমাণুকে আঘাত করলে সেগুলিও আবার ইলেক্ট্রন পজিট্রনের জোড়া সৃষ্টি করে। সুতরাং পাওয়া যায় একটি ইলেক্ট্রন বর্ষণ। এর ফলে এক রকম আলোক সৃষ্টি হয় যার নাম চেরেনকভ (Cerenkov) বিকিরণ। সুতরাং রাতের আকাশে আলোর ঝলক দেখে গামা রশ্মি বিস্ফোরণের নির্দেশ পাওয়া যায়। অবশ্য অন্য কয়েকটি পরিঘটনা থেকেও আকাশে আলোর ঝলক দেখা যেতে পারে। যেমন, বিদ্যুৎ চমকানো, পড়ন্ত (tumbling) কৃত্রিম উপগ্রহে প্রতিফলিত সূর্যালোক এবং কক্ষপথে প্রদক্ষিণরত কৃত্রিম উপগ্রহের ধ্বংসাবশেষ। যথেষ্ট দূরস্থিত দুটি স্থানে দুই কিম্বা ততোধিক আলোর ঝলক যুগপৎ পর্যবেক্ষণ করে গামা রশ্মির বিস্ফোরণ এবং উপরে উল্লিখিত অভিক্রিয়াগুলির (effects) ভিতর পার্থক্য বোঝা সম্ভব। নীল পোর্টার (Neil Porter) এবং ট্রেভর উইকস (Trevor Weekes) নামে ডাবলিনের দুই বৈজ্ঞানিক অ্যারিজোনাতে (Arizona) টেলিস্কোপের সাহায্যে এই ধরণের অনুসন্ধান করেছিলেন। তাঁরা অনেকগুলি আলোর ঝলক দেখতে পেয়েছিলেন কিন্তু কোনোটিকে আদিম কৃষ্ণগহ্বর থেকে নির্গত গামা রশ্মি বিস্ফোরণের ফলে হয়েছে বলে নিশ্চিত সিদ্ধান্ত করতে পারেন নি।
আদিম কৃষ্ণগহ্বর অনুসন্ধানের চেষ্টা হয়তো বিফল হবে বলে মনে হয় কিন্তু তাহলেও এই প্রচেষ্টার ফলে মহাবিশ্বের আদিম অবস্থা সম্পর্কে গুরুত্বপূর্ণ সংবাদ আমরা পাব। আদিম অবস্থায় মহাবিশ্ব যদি বিশৃঙ্খল কিম্বা নিয়মহীন থাকত কিম্বা যদি পদার্থের চাপ খুব কম থাকত তাহলে গামা রশ্মির পশ্চাৎপট সম্পর্কে আমাদের পর্যবেক্ষণ থেকে আদিম কৃষ্ণগহ্বরের সংখ্যায় যে সীমা আগে নির্ধারণ করা হয়েছে তার চাইতে অনেক বেশি সংখ্যক আদিম কৃষ্ণগহ্বর উৎপাদন আশা করা যেত। শুধুমাত্র আদিম মহাবিশ্ব যদি মসৃণ ও সমরূপ হোত এবং যদি তার উচ্চচাপ থাকত, একমাত্র তাহলেই পর্যবেক্ষণযোগ্য কৃষ্ণগহ্বরের অভাব ব্যাখ্যা করা সম্ভব।
কৃষ্ণগহ্বর থেকে বিকিরণ বিষয়ক চিন্তাধারা মূলগতভাবে এ শতাব্দীর দুটি মহান তত্ত্ব-ব্যাপক অপেক্ষবাদ (general relativity) এবং কণাবাদী বলবিদ্যার (quantum mechanics) উপর নির্ভরশীল ভবিষ্যদ্বাণীর প্রথম উদাহরণ। তদানীন্তন প্রচলিত দৃষ্টিভঙ্গির বিপরীত হওয়ার জন্য শুরুতে এই মতবাদ প্রচার বিরুদ্ধতা সৃষ্টি করে। “কৃষ্ণগহ্বর থেকে কিছু নির্গত হওয়া কি করে সম্ভব?” অক্সফোর্ড আছে রাদারফোর্ড অ্যাপলটন (Rutherford Appleton) ল্যাবরেটরীতে একটি কনফারেন্সে যখন আমি যখন আমার গণনার ফল ঘোষণা করেছিলাম তখন সাধারণভাবে সবাই আমাকে অবিশ্বাস করেছে। আমার বক্তৃতার পর ঐ অধিবেশনের চেয়ারম্যান লন্ডনের কিংস কলেজের জন জি. টেলর (John G. Taylor) দাবী করলেন পুরো ব্যাপারটাই অর্থহীন। এই মতের ভিত্তিতে তিনি একটি প্রবন্ধও লিখেছিলেন। শেষ পর্যন্ত জন টেলর সমেত অধিকাংশ লোকই এই সিদ্ধান্তে এসেছিলেন যে, ব্যাপক অপেক্ষবাদ এবং কণাবাদী বলবিদ্যা সম্পর্কিত অন্যান্য ধারণা যদি সঠিক হয় তাহলে অন্যান্য উত্তপ্ত বস্তুপিন্ডের মতো কৃষ্ণগহ্বরকেও বিকিরণ করতেই হবে। সুতরাং আমরা যদিও একটিও আদিম কৃষ্ণগহ্বর খুঁজে পাইনি, তবুও কৃষ্ণগহ্বর খুঁজে পেলে তা থেকে যে প্রচুর পরিমাণ গামা রশ্মি এবং এক্স-রে নির্গত হতে দেখা যাবে সে বিষয়ে সাধারণ মতৈক্য রয়েছে।
মনে হয়, কৃষ্ণগহ্বর থেকে বিকিরণের অস্তিত্বের অন্তর্নিহিত অর্থ হল মহাকর্ষের ফলে চুপসে যাওয়াই কৃষ্ণগহ্বরের চরম এবং অপরিবর্তনীয় পরিণতি নয়। কিন্তু আগে ঐ রকম চিন্তাধারাই ছিল। কোনো মহাকাশচারী যদি কৃষ্ণগহ্বরে পতিত হন তাহলে কৃষ্ণগহ্বরটির ভর বৃদ্ধি পাবে কিন্তু ঐ বাড়তি ভরের তুল্য মনের শক্তি বিকিরণ রূপে মহাবিশ্বে ফিরে আসবে। সুতরাং এক অর্থে মহাকাশচারীটি চক্রাকারে আবার ফিরে আসবে (recycle); কিন্তু এই অমরত্ব হবে একটু মন্দ ধরনের। কারণ, মহাকাশচারীটি কৃষ্ণগহ্বরের ভিতর ছিঁড়ে টুকরো টুকরো হয়ে যাওয়ার সময় তার ব্যক্তিগত কালবোধ যে লোপ পাবে সেটা প্রায় নিশ্চিত। এমন কি, শেষ পর্যন্ত যে ধরনের কণা কৃষ্ণগহ্বর থেকে নির্গত হবে সেগুলিও মহাকাশচারী যে কণাগুলি দিয়ে গঠিত হয়েছিল সাধারণত তার চাইতে পৃথক হবে। একমাত্র যা বেঁচে থাকবে সেটি হল মহাকাশচারীটির ভর বা শক্তি।
যতক্ষন পর্যন্ত কৃষ্ণগহ্বরটির ভর এক গ্রামের ভগ্নাংশের চাইতে বেশি থাকবে ততক্ষণ পর্যন্ত কৃষ্ণগহ্বর থেকে বিকিরণ (emission) নির্ণয় করার জন্য যে আসন্নতাগুলি (approximations) আমি ব্যবহার করেছি সেগুলি ভালই কার্যকর হবে। কিন্তু কৃষ্ণগহ্বরের জীবনকালের শেষে যখন তার ভর অতিক্ষুদ্র হয়ে যাবে তখন এই আসন্নতাগুলি ভেঙ্গে পড়বে। সবচাইতে সম্ভাব্য ভবিষ্যৎ মনে হয়ঃ কৃষ্ণগহ্বরটি অদৃশ্য হয়ে যাবে- অন্ততপক্ষে মহাকাশের আমাদের অঞ্চল থেকে। তার সঙ্গে নিয়ে যাবে ওই মহাকাশচারীটিকে এবং সত্যিই যদি আর কোনো অনন্যতা (singularity) তার ভিতর থেকে থাকে তাহলে সেটিকেও। ব্যাপক অপেক্ষবাদ যে অনন্যতাগুলি সম্পর্কে ভবিষ্যদ্বাণী করেছিল কণাবাদী বলবিদ্যা যে সেগুলিকে দূর করতে পারে এটাই ছিল তার প্রথম ইঙ্গিত। কিন্তু ১৯৭৪ সালে আমি এবং অন্যান্য অনেকে যে পদ্ধতি ব্যবহার করছিলাম, তা থেকে কণাবাদী মহাকর্ষে অনন্যতাগুলি দেখা দেবে কি না- এই জাতীয় প্রশ্নের উত্তর মেলে না। সুতরাং ১৯৭৫ সালের পর থেকে আমি রিচার্ড ফেনম্যানের (Richard Feynman) ইতিহাসের যোগফলের (sum of histories) চিন্তাধারার ভিত্তিতে আরো জোরের সঙ্গে কণাবাদী মহাকর্ষের সমীপবর্তী হতে শুরু করেছি। এই পদ্ধতিতে মহাবিশ্ব এবং মহাকাশচারীর মতো তার আধেয়র (contents) উৎপত্তি এবং পরিণতি সম্পর্কে যে ইঙ্গিত পাওয়া যায় তার বিবরণ দেওয়া হবে পরবর্তী দুই অধ্যায়ে। আমরা দেখব যদিও অনিশ্চয়তাবাদ সমস্ত ভবিষ্যদ্বাণীর নির্ভুলতাকে সীমিত করে তবুও এ তত্ত্ব একই সঙ্গে স্থান-কালের অনন্যতার মূলগত অনিশ্চয়তা (unpredictability) হয়তো দূরীভুত করে।
“কালের সংক্ষিপ্ত ইতিহাস” বই সম্পর্কিত আপনার মন্তব্যঃ