নিউটনের মহাকর্ষ সূত্রে সময়ের কোন উল্লেখ ছিল না। সময়ের ব্যাপারটা আসলে বেশ গুরুত্বপূর্ণ। মহাকর্ষের টান বুঝবার জন্য নিউটনের সূত্রই যথেষ্ট (প্রথম পর্ব দ্রষ্টব্য), কিন্তু কেউ যদি প্রশ্ন করে যে, এই টান অনুভব করতে কতটা সময় লাগবে, তা হলেই কিন্তু বিপদ! নিউটনের মহাকর্ষ-সূত্র এই প্রশ্নের সঠিক উত্তর দিতে পারবে না।
ব্যাপারটা আরেকটু পরিস্কার করা যাক। আমরা জানি যে, আমরা জানি যে, পৃথিবী নামের আমাদের এই গ্রহটি অনবরত ঘুরে চলেছে সূর্যের চারদিকে (দ্বিতীয় পর্ব দ্রষ্টব্য)। পৃথিবী থেকে সূর্যের দুরত্বও বিজ্ঞানীরা অংক কষে বের করেছেন প্রায় ১৫ কোটি কিলোমিটার (খুব সঠিক ভাবে বলতে গেলে অবশ্য ১৪ কোটি ৯৫ লক্ষ ৯৭ হাজার ৮৭০কি. মি )। এখন মনে করা যাক, বিরাট একটা মহাজাগতিক বস্তু এসে হঠাৎ ধাক্কা দিল সূর্যকে। এই ধাক্কার ফলে সূর্য নিজ অবস্থান থেকে বেশ খানিকটা সরে গেল। এর ফলে কি হবে? দূরত্ব বদলে যাওয়ায় মহাকর্ষের টানও যাবে বদলে। তবে প্রশ্ন হল কখন পৃথিবীবাসী জানবে এই ‘টান বদলের’ খবর? নিউটনের সূত্র কিন্তু বলছে সাথে সাথেই। দূরত্ব বদলে যাওয়ার সাথে সাথেই মহাকর্ষের টান যাবে বদলে আর সেই বার্তা সাথে সাথেই পৌছে যাবে পৃথিবীতে । সমস্যাটা আসলে এখানেই। এই সমস্যার ব্যাপারটা নিউটনের আমলে মোটেই বোঝা যায়নি, কারণ এ প্রশ্নই তখন ওঠেনি। আমাদের দৈনন্দিন জীবনে নিউটনের সূত্র দিয়েই দিব্যি কাজ চলে যায়। কিন্তু বিশেষ কিছু পরিস্থিতিতে এসে নিউটনের সূত্র একদম ভেঙ্গে পড়ে। সেই বিশেষ পরিস্থিতির উদ্ভব হয় কখন? কিছু উদাহরণ দেওয়া যাক; কৃষ্ণ গহবরের (Black Hole) কাছাকাছি- যখন মাধ্যাকর্ষণ বল প্রচন্ড বেশী হয় এমনি অবস্থায়, অথবা বস্তু কণা যখন ছুটতে থাকে প্রচন্ড গতিতে -প্রায় আলোর বেগের কাছাকাছি।

আলোর বেগ নিয়ে এখানে দু’ চার কথা অবশ্যই বলা প্রয়োজন। আলোর বেগ কিন্তু আর দশটা সাধারণ বস্তু কণার বেগের মত নয়। বিশাল সে বেগ। সেকেন্ডে প্রায় তিন লক্ষ কিলোমিটার। ৩০০০ কিলোমিটার রাস্তা পেরুতে বিশ্বের সবচেয়ে দ্রুতগামী ট্রেনেরও লাগবে ১০ ঘন্টার বেশী। এরোপ্লেনের লাগবে অন্তত ৩ ঘন্টা। সেখানে আলোর লাগে ১ সেকেন্ডের ১০০ ভাগের এক ভাগ মাত্র। এই আলো নিয়ে চিন্তা করতে করতেই যুগান্তকারী এক তত্ত্ব দিলেন আইনস্টাইন ১৯০৫ সালে। তত্ত্বটির নাম ‘আপেক্ষিকতার বিশেষ তত্ত্ব’ (Special theory of Relativity)। আইনস্টাইন তখন সবে মাত্র তার পি.এইচ.ডি শেষ করেছেন সুইজারল্যান্ডের জুরিখ বিশ্ববিদ্যালয় থেকে। তিনি তখন বার্ণ এ একটি পেটেন্ট অফিসে তৃতীয় শ্রেনীর কেরানী হিসেবে কর্মরত। এই চাকরীটি এমনিতেই পেয়ে যাননি আইনস্টাইন – পেয়েছিলেন তাঁর এক বন্ধু গ্রসম্যানের (উনার কথা এই প্রবন্ধের শেষদিকে আবার উল্লেখ করা হবে; আইনস্টাইনের জীবনে তাঁর অবদান অসামান্য। আইনস্টাইন তাঁর পি.এইচ.ডি থিসিস এই গ্রসম্যানের নামে উৎসর্গ করেন) বাবার সুপারিশে। এই পেটেন্ট অফিসে কর্মরত থাকা অবস্থাতেই আইনস্টাইন অবসর সময়ে তিনটি যুগান্তকারী পেপার (একটি ফটো-ইলেকট্রিক তত্ত্বের উপর প্লাঙ্কের ধারণাকে সঙ্কলিত করে, আরেকটি আপেক্ষিকতার বিশেষ তত্ত্বের উপর, আর অন্যটি পরিসংখ্যান বলবিদ্যার উপর) প্রকাশ করলেন যা এক ধাক্কায় এই চিরায়ত বিশ্বজগৎ সম্বন্ধে আমাদের এতদিনকার ধ্যান- ধারণাকে আমূল পালটে দিল।
আপেক্ষিকতার বিশেষ তত্ত্বটি নিয়ে একটু বিষদ আলোচনা করা যাক। এই তত্ত্বের ভিত্তি গড়ে উঠেছে আসলে ১৮৮৭ সালে আমেরিকান দুই পদার্থবিদের (মাইকেলসন এবং মর্লি) পরীক্ষা থেকে প্রাপ্ত সিদ্ধান্ত থকে – ‘আলোর বেগ তার উৎস বা পর্যবেক্ষকের গতির উপর কখনই নির্ভর করে না; সব সময়ই ধ্রুবক।’ ব্যাপারটা খুবই অদ্ভুত। মন মানতে চায় না; কারণ এই ব্যাপারটি বস্তুর বেগ সংক্রান্তআমাদের সাধারণ পর্যবেক্ষনের একেবারেই বিরোধী। যেমন ধরা যাক, আপনি একটি রাস্তায় ৪০ কি.মি বেগে গাড়ী চালাচ্ছেন। আপনার বন্ধু ঠিক বিপরীত দিক থেকে আরেকটি গাড়ী নিয়ে ৪০ কি.মি বেগে আপনার দিকে ধেয়ে এল। আপনার কাছে কিন্তু মনে হবে আপনার বন্ধু আপনার দিকে ছুটে আসছে দ্বিগুন ( ৪০ + ৪০ = ৮০ কি.মি) বেগে। আলোর ক্ষেত্রে ব্যাপারটা অন্যরকম। ধরা যাক, একজন পর্যবেক্ষক সেকেন্ডে ১ লক্ষ ৫০ হাজার কিলোমিটার বেগে আলোর উৎসের দিকে ছুটে চলেছে। আর উৎস থেকে আলো ছড়াচ্ছে তার নিজস্ব বেগে – অর্থাৎ সেকেন্ডে প্রায় ৩ লক্ষ কিলোমিটারে। এখন কথা হচ্ছে পর্যবেক্ষকের কাছে আলোর বেগ কত বলে মনে হওয়া উচিৎ? আগের উদাহরন থেকে পাওয়া অভিজ্ঞতা বলে – সেকেন্ডে (১ লক্ষ ৫০ হাজার + ৩ লক্ষ =) ৪ লক্ষ ৫০ হাজার কিলোমিটার। আসলে কিন্তু তা হবে না। পর্যবেক্ষক আলোকে সেকেন্ডে ৩ লক্ষ কিলোমিটার বেগেই তার দিকে আসতে দেখবে। এটাই মাইকেলসন এবং মর্লির ব্যতিক্রমী পর্যবেক্ষণ আলোর গতি সব সময়ই একই রকম (ধ্রুবক)।
আইনস্টাইনের এই থিওরী আলোচনা করবার জন্য গনিতের যে জ্ঞান থাকা দরকার হয় তা একেবারেই প্রাথমিক স্তরের। স্কুল কলেজে যারা বীজগনিত পড়ছে তারাও বুঝতে পারবে অংকগুলো। কিন্তু অংক থেকে যে সিদ্ধান্তগুলো (mass increase, length contraction আর time dialation) বেরিয়ে আসে তা সত্যই আশ্চর্য জনক। যদি কোন বস্তু কণার বেগ বাড়তে বাড়তে আলোর গতিবেগের কাছাকাছি চলে আসে, বস্তুটির ভর বেড়ে যাবে নাটকীয় ভাবে (mass increase), দৈর্ঘ্য সঙ্কুচিত হয়ে যাবে (length contraction) এবং সময় ধীরে চলবে (time dialation)। আরেকটা জিনিস বেরিয়ে আসল আইনস্টাইনের তত্ত্ব থেকে। শুন্য পথে আলোর যা গতিবেগ, কোন বস্তুর গতিবেগ যদি তার সমান বা বেশী হয়, তবে সমীকরণগুলো নিরর্থক হয়ে পড়ে। এ থেকে একটা সিদ্ধান্ত করা হয়েছে কোন পদার্থই আলোর সমান গতিবেগ অর্জন করতে পারবে না। সেই থেকে মহাবিশ্বের গতির সীমা নির্ধারিত হয় আলোর বেগ দিয়ে।
এখন প্রবন্ধের শুরুর সমস্যাটায় আবারো ফিরে যাই। নভোজাগতিক বস্তুর ধাক্কায় সূর্য সরে গেল তার আগের অবস্থান থেকে। নিউটনের সূত্র বলছে পৃথিবীবাসীর তা যেনে যাওয়া উচিৎ পরমুহূর্তেই। কিন্তু আপেক্ষিক তত্ত্ব বলছে আলোর চেয়ে কোন কিছুই তাড়াতাড়ি যেতে পারে না। আলোর বেগেও যদি যাওয়া যায়, তবুও সময় লাগে। মহাকাশে দূরত্বের কথা ভাবলে সময়টা নেহাত ফেলনাও নয়। আলোর গতিতে ১৫ কোটি কিলোমিটার রাস্তা পেরুতে সময় ৮ মিনিটের কিছু বেশী। এ তো গেল সূর্যের কথা। তারাদের মধ্যে যেটি আমাদের সবচেয়ে কাছের, সেই প্রক্সিমা সেন্টরী থেকে আলো আসতে সময় লাগে চার বছরেরও বেশী। অর্থাৎ এই মুহূর্তে যদি কোন কারণে তারাটা ধ্বংস হয়ে যায়, আমরা তা জানব আজ থেকে চার বছর পর!
নিউটনের সূত্রের সাথে আরেকটি সূত্রের কিন্তু খুব মিল রয়েছে। কুলম্বের সূত্র। ১৭৮০ এর দিকে নিউটনের প্রিন্সিপিয়া প্রকাশের প্রায় শত-বর্ষ পরে শার্ল কুলম্ব দেখালেন, দুটি জিনিসে বৈজ্ঞানিক চার্জ থাকলে তাদের মধ্যে একটা আকর্ষণ বা বিকর্ষণ বল কাজ করবে। মহাকর্ষের মত এখানে একতরফা আকর্ষণ নয়, বিকর্ষণ ও হতে পারে; তবে আকর্ষণ নাকি বিকর্ষণ – তা নির্ভর করবে চার্জ গুলোর ধর্মের (সমধর্মী নাকি বিপরীতধর্মী) উপর। কিন্তু এদের মধ্যে বলের জোর কতটা? কুলম্ব সেখালেন দূরত্ব বাড়ালে এই বল বর্গের অনুপাতে কমে যায়। আর দূরত্ব ঠিক রেখে যদি বাড়ানো হয় চার্জের পরিমান, তবে বলের পরিমানও বাড়তে থাকবে তার গুনফলের অনুপাতে। ঠিক মহাকর্ষের মতই দারাচ্ছে ব্যাপারটা। উনবিংশ শতকের প্রথমার্ধে চুম্বক নিয়ে গবেষনা করতে গিয়ে ফ্যারাডে দেখালেন, কোন একটা জায়গায় যদি চুম্বকের টানের কমা-বাড়া হয় – তাহলে সেখানে একটা বৈদ্যুতিক কারেন্টের সৃষ্টি হয়। এই আবিস্কারের উপর নির্ভর করেই কিন্তু পরবর্তীতে আবিস্কার করা হয়েছিল ডায়নামো বা জেনারেটর। আমরা যদি আজ কুলম্বের যুগেই পড়ে থাকতাম তবে মহাকর্ষ আর আপেক্ষিতত্ত্বের মধ্যকার বিরোধের মত এই সূত্রের বিরোধ নিয়েও মাথা ঘামাতে হত। এই মাথা-ব্যথা থেকে আগেই মুক্তি দিয়ে গেছেন ম্যাক্সওয়েল বলে এক বিজ্ঞানী। তিনি বললেন, বিদ্যুৎ আর চুম্বকের কথা আলাদা করে বললে হবে না, বলতে হবে এক সঙ্গে – তড়িচ্চুম্বক। নিউটনের প্রায় দু’শ বছর পর এভাবে নতুন করে সমন্বয়ের রাস্তা দেখিয়ে ম্যাক্সওয়েল বললেন, ঢেউয়ের মত প্রবাহিত হয়ে ছড়িয়ে পড়ে বিদ্যুৎ আর চুম্বক সংক্রান্ত যাবতীয় সংবাদ।
মহাকর্ষ সূত্রেরও যদি ঠিক একই রকম একটা ভাষ্য পাওয়া যেত, তাহলে আপেক্ষিকতার সাথে বিরোধ থাকত না কখনও। কিন্তু বিংশ শতাব্দীর গোড়ায় এসেও দেখা গেল নিউটনের সূত্র দিয়ে দিব্যি কাজ চালিয়ে নেওয়া যাচ্ছে। আইনস্টাইন নিজেই নামলেন তখন এই বিরোধ মেটানোর কাজে। এবার কিন্তু অংকের ব্যাপারটা আর স্কুল-কলেজ পর্যায়ে সীমাবদ্ধ রইল না। স্কুল-কলেজ তো অনেক ছোটট ব্যাপার, সে সময় পদার্থ-বিদ্যার উচ্চতম পাঠ নিতে হলে অংকের যে জ্ঞান দরকার তাতেও কাজ চলল না। আইনস্টাইনকে এর জন্য শিখতে হল এক নতুন ধরনের জ্যামিতি। মার্সেল গ্রসম্যান নামে আইনস্টাইনের এক বন্ধু ছিলেন জুরিখে, অংকের পন্ডিত। তাঁর থেকেই এই নতুন ধরনের জ্যামিতি শিখলেন আইনস্টাইন। আমরা সেই জ্যামিতিকে বাংলায় বলতে পারি ‘সমদেশ জ্যামিতি’। কি রকম সেই জ্যামিতি? আর পুরোন জ্যামিতির সাথে তার পার্থক্যইটা বা কোথায়? আসলে স্কুলে আমরা যে জ্যামিতি শিখি তা হল ‘ইউক্লিডিয়ান জ্যামিতি’ যার অন্য আরেকটা নাম –‘সমতল জ্যামিতি’। এই সমতল জ্যামিতিতে কতকগুলো স্বতঃসিদ্ধ রয়েছে। যেমন ত্রিভুজের তিন কোনের সমষ্টি সব সময়ই ১৮০ ডিগ্রী হবে; দুটি সমান্তরাল রেখা কখনই একসাথে মিলবে না; বৃত্তের পরিসীমা (circumference) পাওয়া যাবে ঢ এবং ডায়ামিটারের গুনফল থেকে; ইত্যাদি। এগুলো সবই আমরা ছোটবেলায় পড়েছি। তবে এই স্বতঃসিদ্ধগুলো গুলো শুধু সমতলের (flat surface) ক্ষেত্রেই প্রযোজ্য। সমতলের বদলে বক্রতলে (curved surface) এসে কিন্তু এই ইউক্লিডিয়ান জ্যামিতির স্বতঃসিদ্ধগুলো একদম ভেঙ্গে পড়ে। এই পরিস্থিতিতে (অর্থাৎ বক্রতলে) ) কিন্তু দুটি সমান্তরাল রেখা একসাথে মিলে যেতে পারে কিংবা ত্রিভুজের তিন কোনের সমষ্টি ১৮০ ডিগ্রীর চেয়ে কম বা বেশী হতে পারে। নীচের ছবিটা দেখলে হয়ত পাঠকদের কাছে ব্যাপারটা আরও পরিস্কার হবে।
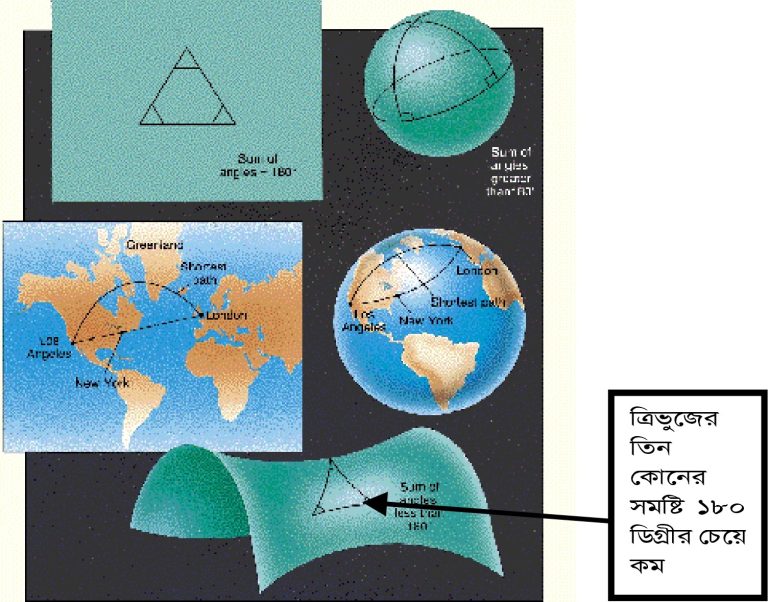
আইনস্টাইন এই সমদেশ জ্যামিতি গ্রসম্যানের কাছ থেকে শিখে অবশেষে মহাকর্ষের এক নতুন তত্ত্ব দিলেন -১৯১৫ সালে। যে তত্ত্বের সাহায্যে মহাকর্ষের সাথে আপেক্ষিকতাকে সন্নিবদ্ধ করলেন আইনস্টাইন তাকে বলা হল ‘আপেক্ষিকতার ব্যাপক তত্ত্ব’ (General Theory of Relativity)। আইনস্টাইন দেখালেন যে, মহাকর্ষকে শুধু শুন্যস্থানে দুটি বস্তুর মধ্যে আকর্ষণ বল (নিউটন যেভাবে চিন্তা করেছিলেন) হিসেবে ভাবলে চলবে না, ভাবতে হবে আপাতঃ শক্তি (aparent force) হিসেবে যার উদ্ভব হয় আসলে মহাশুন্যের (space) নিজস্ব বক্রতার কারণে। মহাশুন্যের এই বক্রতাকে বুঝবার জন্য মহাশুন্যকে একটা পাতলা রাবারের আচ্ছাদনে (rubber sheet) তৈরী টেবিলের উপরিভাগের সাথে তুলনা করা যেতে পারে (সহজ কথায়, আপনার ঘরের টেবিলের উপরটা কাঠ নয়, পাতলা রাবারের তৈরী বলে এ মুহূর্তে ভেবে নিন)। সাধারণ (ভরহীন) অবস্থায় একটি বস্তুকণা গতিশীল হলে এই আচ্ছাদনের উপর দিয়ে সরল রেখাতেই চলবে। কিন্তু একটা ওজনদার বস্তুকে (ধরা যাক একটা ভারী পাথরখণ্ড) যদি আচ্ছাদনের উপর চাপিয়ে দেওয়া হয়, তবে সেই রবারের আচ্ছাদনটির আকার বিকৃত হয়ে যাবে -বেঁকে যাবে অনেকটা নীচের ছবির মত।
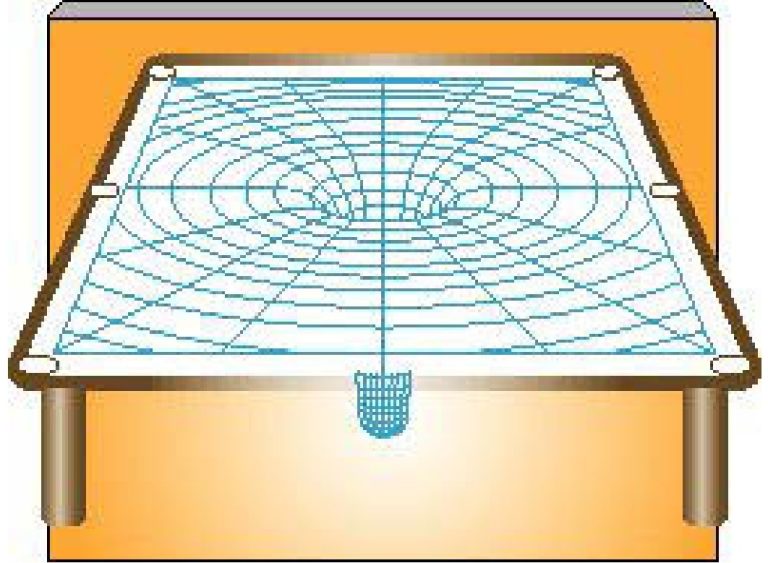
যত ভারী পাথর চাপানো হবে, বক্রতাও বেড়ে যাবে সেই অনুপাতে। এখন কোন বস্তুকণা কে আচ্ছাদনের উপর ছেড়ে দিলে এর চলার পথও কিন্তু বেঁকে যাবে আচ্ছাদনের উপরিভাগের এই বক্রতার কারণে। এই তত্ত্বের আবেদন কিন্তু সুদূর-প্রসারী। বিশাল ভরের কারণে একই ভাবে মহাশুন্যে সৃষ্টি হয় বক্রতা যা কোন বস্তুকণার গতিপথকে – এমনকি আলোর গতিপথকেও বাঁকিয়ে দেয়। আমাদের সৌরজগতের কেন্দ্রে সূর্য থাকার কারণেও কিন্তু সৃষ্টি হয়েছে বক্রতা যার কারণে পৃথিবী সহ অন্যান্য গ্রহগুলোকে একটি বক্রতলে সূর্যের চারদিকে ঘুরতে দেখা যায়। প্রফেসর আর্কিবালড হুইলারের ভাষায় -‘পদার্থ স্পেসকে বলছে কিভাবে বাঁকতে হবে, আর স্পেস পদার্থকে বলছে কিভাবে চলতে হবে’! এটাই আসলে নিউটনের মহাকর্ষকে আইনস্টাইনের চোখ দিয়ে দেখা।
তাহলে ‘আপেক্ষিকতার ব্যাপক তত্ত্ব’ থেকে আমরা জানলাম – সবকিছুই এমনকি আলোও মহাশুন্যের এই বক্রতার (মহাকর্ষের) কারণে প্রভাবিত হয়। ১৯১৫ সালে তাঁর তত্ত্বটি প্রকাশ করার পর পরই আইনস্টাইন বললেন, সূর্যের কাছাকাছি কোন তারা থেকে আলো পৃথিবীতে আসার সময় সূর্যের আকর্ষণের কারণে বেঁকে যাওয়ার কথা। ঠিক কতখানি বাঁকবে তাও আইনস্টাইন গণনা করে দেখালেন ১.৭৫ ডিগ্রী। খুবই ছোট- কিন্তু পরিমাপযোগ্য তো বটেই। কিন্তু সমস্যাটা হল, আইনস্টাইনের কথা ঠিক কিনা তা বোঝা যাচ্ছিল না তখন। এর কারণও আছে। সাধারণ অবস্থায় সূর্যের কাছাকাছি কোন তারা খুঁজে বের করাই মুশকিল। সূর্যগ্রহণের সময়, যখন চাঁদের ছায়ায় সূর্য ঢেকে যায়, তখনই কেবলমাত্র এধরনের পরীক্ষা-নিরীক্ষা আর পর্যবেক্ষণ করে সত্য-মিথ্যা বের করা সম্ভব। তাই করা হল। ১৯১৯ সালের ২৯শে মে স্যার আর্থার এডিংটনের নেতৃত্বে এক দল জ্যোতির্বিদ সূর্যগ্রহনের সময় তারার আলোর এই বিক্ষেপণ পরিমাপ করলেন ব্রাজিলে। ফলাফল কিন্তু আইনস্টাইনের ভবিষ্যদ্বানীর সাথে অবিকল মিলে গেল!
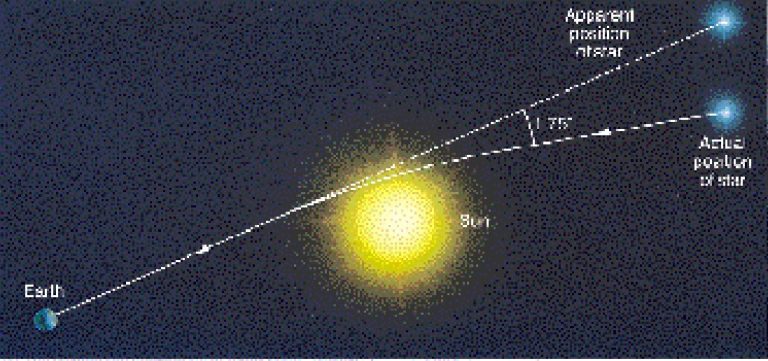
রাতারাতি আইনস্টাইন পৌঁছে গেলেন খ্যাতির শিখরে। তার পূর্ববর্তী সকল অবদানের কথা মনে রেখেও বলা যায় – এই একটি মাত্র ভবিষ্যদ্বানীর সাফল্য তাকে তখনকার সময়ের অন্যতম শ্রেষ্ঠ বিজ্ঞানীর আসনে পাকাপোক্তভাবে বসিয়ে দিল! ১৯২১ সালে আইনস্টাইন পদার্থবিজ্ঞানে তার অবদানের স্বীকৃতি স্বরূপ নোবেল পুরস্কার লাভ করেন – তবে আপেক্ষিক তত্ত্বের জন্য নয়, তার photoelectric effect (১৯০৫) এ অবদানের জন্য।
তাহলে মহাকর্ষ নিয়ে কোন বিরোধটা মিটালেন আইনস্টাইন? আসলে ঠিক বিরোধ নয়, বলা যায় নিউটনের মহাকর্ষ সূত্রকে আপেক্ষিকতত্ত্বের মাধ্যমে আইনস্টাইন আরও ব্যাপকতা দিলেন। যখন বস্তুর গতিবেগ থাকে অল্প, অথবা মাধ্যাকর্ষণের প্রভাব থাকে সামান্য, তখন আসলে নিউটন এবং আইনস্টাইনের তত্ত্ব একই রকম ফলাফলই দেয়। কোন বিরোধ থাকে না। তবে বিশেষ কিছু ক্ষেত্রে – যেমন সূর্যের কাছাকাছি অবস্থিত তারার আলোর বিক্ষেপণ (উপরে বর্ণিত) নিউটনের সূত্র দিয়ে মোটেই ব্যাখ্যা করা যায় না, যা আপেক্ষিক তত্ত্বের মাধ্যমে খুব সহজেই করা যাচ্ছে। আবার, বুধ গ্রহের কক্ষপথ নির্ণয়ে নিউটনের সূত্র বরাবরই কিছুটা ভুল ফলাফল দিচ্ছিল যার ফলে বিজ্ঞানীরা সূর্য আর বুধের মাঝে আরেকটি গ্রহের অবস্থান কল্পনা করছিলেন (এমনকি এই অদৃশ্য গ্রহটির নামও দেওয়া হয়েছিল ‘ভালকান’)। পরবর্তীতে আইনস্টাইনের সূত্রের সাহায্যেই বিজ্ঞানীরা সঠিকভাবে বুধ গ্রহের কক্ষপথ নির্ণয় করেছিলেন। ভালকানকে কল্পনা করার আর কোন প্রয়োজন রইল না।
বিশ্বজগৎ সম্বন্ধে আমাদের ধারণা কি এখন ক্রমশঃ স্পষ্ট হয়ে উঠছে? কোপার্নিকাসের সূর্যকেন্দ্রিক বিপ্লবের পর গ্যলিলিওর নভোজাগতিক বস্তুনিয়ে গবেষণা আর তাঁর পর্যবেক্ষণ গুলো পরবর্তীতে নিউটনের গ্রহ-নক্ষত্রের গতিপথ নিয়ে চিন্তা ভাবনার পথ সুগম করে দেয়। নিউটন মহাকর্ষ সূত্রের সাহায্যে দেখালেন – মহাবিশ্বের প্রতিটি বস্তুকণাই প্রাকৃতিক নিয়ম মেনে চলে। আর আইনস্টাইন এসে এই মহাকর্ষকে ব্যাখ্যা করেলন সম্পুর্ন নতুন ভাবে – মহাশুন্যের বক্রতা (bent time-space) দিয়ে। বললেন, মহাশুন্য রাবারের প্লেটের মতই বেঁকে যায়- যার প্রভাব থেকে আলোও মুক্তি পায় না। ১৯১৯ সালে এডিংটনের পরীক্ষা আইনস্টাইনের তত্ত্বেরই সত্যতা প্রমাণ করল। এখানেই শেষ নয় – আইনস্টাইনের এই আপেক্ষিক তত্ত্বই পরবর্তীতে কৃষ্ণ গহবরের অস্তিত্ব আর মহাবিশ্বের প্রসারণকে সঠিক ভাবে ব্যাখ্যা করেছিল। উন্মোচিত হয়েছিল রহস্যের আর এক আকর্ষনীয় অধ্যায়।
“আলো হাতে চলিয়াছে আঁধারের যাত্রী” বই সম্পর্কিত আপনার মন্তব্যঃ