বৈজ্ঞানিক তত্ত্বগুলির সাফল্য, বিশেষ করে, নিউটনীয় মহাকর্ষীয় তত্ত্বের সাফল্যের ফলে ঊনবিংশ শতাব্দীর প্রথম দিকে ফরাসী বৈজ্ঞানিক মারকুইস দা লাপ্লাস (Marquis De Laplace) যুক্তি দেখিয়েছিলেন- মহাবিশ্ব সম্পূর্ণভাবে নির্ধারণীয় (বৈজ্ঞানিক নিয়তিভিত্তিক- deterministic)। লাপ্লাসের প্রস্তাবনা ছিল, এমন একগুচ্ছ বৈজ্ঞানিক বিধি থাকা উচিত যা সাহায্যে মহাবিশ্বের যে কোন সময়কার অবস্থা যদি সম্পূর্ণভাবে জানা থাকে, তাহলে ভবিষ্যতে মহাবিশ্বে কি ঘটবে সে সম্পর্কে সম্পূর্ণ ভবিষ্যদ্বাণী করা সম্ভব হবে। উদাহরণঃ সূর্য এবং গ্রহগুলোর যে কোন এক সময়কার দ্রুতি এবং অবস্থান যদি জানা থাকে, তাহলে নিউটনের বিধিগুলির সাহায্যে সৌরতন্ত্রের অন্য যে কোন সময়কার অবস্থা গণনা করে বলা সম্ভব। এক্ষেত্রে নির্ধারণীয়তাবাদ (determinism) বেশ স্পষ্ট। কিন্তু লাপ্লাস আরো খানিকটা অগ্রসর হয়েছিলেন। তাঁর অনুমান ছিল, অন্য সমস্ত বিষয় সম্পর্কে, এমন কি, মানবিক আচরণ সম্পর্কেও এই ধরণের বিধি রয়েছে।
অনেকেই বৈজ্ঞানিক নির্ধারণীয়তাবাদের (determinism) ঘোর বিরোধী ছিলেন। তাঁরা মনে করতেন, এই মতবাদ পৃথিবীতে ঈশ্বরের হস্তক্ষেপের স্বাধীনতায় হস্তক্ষেপ করে। কিন্তু, তবুও এই শতাব্দীর প্রথম দিক পর্যন্ত নির্ধারণীয়তাবাদই ছিল প্রমাণ (standard) বৈজ্ঞানিক অনুমান। এই বিশ্বাস পরিত্যাগ করতে হবে- এই সম্পর্কে প্রথম ইঙ্গিতগুলির একটি ছিল ব্রিটিশ বৈজ্ঞানিক লর্ড র্যালে (Lord Rayleigh) এবং স্যার জেমস জিনসের (Sir James Jeans) গণনা। সে গণনায় দেখা যায়, যে কোন উত্তপ্ত বস্তুপিন্ড কিম্বা তারকার মত একটি বস্তুপিন্ড আবশ্যিকভাবে অসীম হারে শক্তি বিকিরণ করবে। তখন আমরা যা বিশ্বাস করতাম, সেই বিধি অনুসারে একটি উত্তপ্ত বস্তুপিন্ডের সমভাবে সমস্ত স্পন্দাংকে বিদ্যুৎ-চুম্বকীয় তরঙ্গ (eletro magnetic wave) [যেমন, বেতার তরঙ্গ, দৃশ্যমান আলোক, কিম্বা এক্স-রে] বিকিরণ হওয়া উচিত। উদাহরণঃ একটি উত্তপ্ত বস্তুপিন্ড সেকেন্ডে এক থেকে দুই মিলিয়ন মিলিয়ন তরঙ্গের স্পন্দাংকে যে পরিমাণ শক্তি বিকিরণ করে, সেই একই পরিমাণ শক্তি তার সেকেন্ডে দুই থেকে তিন মিলিয়ন মিলিয়ন তরঙ্গের স্পন্দাংকেও বিকিরণ করা উচিত। যেহেতু প্রতি সেকেন্ডে তরঙ্গের সংখ্যা অসীম সেজন্য এর অর্থ হবে বিকিরিত (radiated) শক্তির পরিমাণও অসীম।
সুস্পষ্ট হাস্যকর এই ফলশ্রুতি এড়ানোর জন্য জার্মান বৈজ্ঞানিক ম্যাক্স প্লাংক (Max Planck) ১৯০০ খৃষ্টাব্দে প্রস্তাব করেন- আলোক, এক্স-রে এবং অন্যান্য তরঙ্গ যাদৃচ্ছিক (arbitrary) হারে বিকশিত হতে পারে না। বিকিরিত হতে পারে শুধুমাত্র বিশেষ প্যাকেটে (packet), তার নাম তিনি দিয়েছিলেন কোয়ান্টা। তাছাড়া প্রতিটি কোয়ান্টাতেই একটা বিশেষ পরিমাণ শক্তি থাকে এবং তরঙ্গের স্পন্দাংক যত বেশি হয় শক্তিও হয় তত বেশি। সুতরাং যথেষ্ট উচ্চ স্পনাদংক হলে এক একটি কোয়ান্টামের বিকিরণে যে শক্তির প্রয়োজন হবে সেটা প্রাপ্তিযোগ্য শক্তির চাইতে বেশি। সুতরাং উচ্চ স্পন্দাংকের বিকিরণ কমে যাবে। অতএব, বস্তুপিন্ড যে শক্তি ক্ষয় করবে, সেটাও হবে সীমিত।
কোয়ান্টাম প্রকল্প (hypothesis) তপ্ত বস্তুপিন্ডগুলি থেকে বিকিরণ নির্গত হওয়ার পর্যবেক্ষণ করার হার ভালোই ব্যাখ্যা করেছিল। কিন্তু ১৯২৬ সালের আগে পর্যন্ত নির্ধারণীয়তাবাদ (determinism) সাপেক্ষ এই প্রকল্পের ফলশ্রুতি বোঝা যায় নি। সেই সময় ওয়ার্নার হাইজেনবার্গ (Werner Heisenberg) নামে আর একজন জার্মান বৈজ্ঞানিক বিখ্যাত অনিশ্চয়তাবাদ (uncertainly principle) গঠন করেন। একটি কণিকার (particle) ভবিষ্যৎ অবস্থান ও গতিবেগ (velocity) সম্পর্কে ভবিষ্যদ্বাণী করতে হলে তার বর্তমান অবস্থান ও গতিবেগ নির্ভুলভাবে মাপা প্রয়োজন। স্পষ্টতই এ কাজ করার সহজ পন্থা কণাটির উপর আলোকপাত করা। তা হলে কিছু আলোক তরঙ্গকে এ কণিকা বিক্ষিপ্ত (scattered) করে দেবে এবং তার ফলে তার অবস্থানের নির্দেশ পাওয়া যাবে। কিন্তু আলোকের দুটি তরঙ্গশীর্ষের দূরত্বের চাইতে বেশি নির্ভুলভাবে ঐ কণিকার অবস্থান নির্ধারণ করা যাবে না। সেইজন্য প্রয়োজন হবে হ্রস্ব তরঙ্গদৈর্ঘের আলোকপাত করা, যাতে কণিকাটির অবস্থান সঠিকভাবে মাপা যায়। কিন্তু প্ল্যাঙ্কের কোয়ান্টাম প্রকল্প অনুসারে যাদৃচ্ছিক ক্ষুদ্র পরিমাণ আলোক ব্যবহার করা সম্ভব নয়। অন্ততপক্ষে, এক কোয়ান্টাম আলোক ব্যবহার করতে হবে। কিন্তু এই কোয়ান্টাম কণিকাটিকে অস্থির করে তুলবে (disturb) এবং তার গতিবেগে এমন পরিবর্তন আনবে যে সে সম্পর্কে ভবিষ্যদ্বাণী করা যাবে না। তাছাড়া, অবস্থানের মাপন যত নির্ভুল হবে, আলোকের তরঙ্গদৈর্ঘও তত ক্ষুদ্র হবে। সুতরাং এক কোয়ান্টামে শক্তির পরিমাণও হবে উচ্চতর। তা হলে, কণিকাটির গতিবেগের স্থিরত্বকে বৃহত্তর শক্তি বিঘ্নিত করে তুলবে। অন্যভাবে বলা যায়, একটি কণিকার অবস্থান যত নির্ভুলভাবে মাপার চেষ্টা করা যাবে, তার দ্রুতির মাপন হবে তত কম নির্ভুল এবং এর বিপরীতও সত্য হবে (vice versa)। হাইজেনবার্গ দেখিয়েছিলেন কণিকাটির ভরকে তার গতিবেগের অনিশ্চয়তা দিয়ে গুণ করে তাকে কণিকার অবস্থানের অনিশ্চয়তা দিয়ে গুণ করলে গুণফল কখনোই একটি বিশেষ পরিমাণের কম হতে পারে না। এই পরিমাণই প্ল্যাঙ্কের ধ্রুবক (Plank’s constant) বলে পরিচিত। তাছাড়া, এই সীমা কণিকাটির অবস্থান মাপনের চেষ্টার পদ্ধতি কিম্বা গতিবেগ মাপনের চেষ্টার পদ্ধতি কিম্বা কণিকার জাতিরূপের (type) উপর নির্ভরশীল নয়ঃ হাইজেনবার্গের অনিশ্চয়তার নীতি বিশ্বের একটি মূলগত অনতিক্রমনীয় ধর্ম।
পৃথিবী সাপেক্ষ আমাদের দৃষ্টিভঙ্গি সম্পর্কে এই ইনিশ্চয়তার নীতির নিহিতার্থ গভীর। পঞ্চাশ বছরেরও বেশি সময় কেটে গিয়েছে। এখনো বহু দার্শনিক ব্যাপারটার মর্ম সম্পূর্ণভাবে উপলব্ধি করতে পারেন নি এবং এখনো এই অনিশ্চয়তার নীতি বহু দ্বন্দ্বের মূলে রয়েছে। লাপ্লাসের স্বপ্ন ছিল বিজ্ঞানের এমন একটি তত্ত্ব- মহাবিশ্বের এমন একটি প্রতিরূপ যা হবে সম্পূর্ণ নির্ভরযোগ্য (deterministic): মহাবিশ্বের বর্তমান অবস্থানই যদি নির্ভুলভাবে মাপা সম্ভব না হয়, তা হলে ভবিষ্যৎ সম্পর্কে নির্ভুল ভাবে বলা অসম্ভব। এই পরিস্থিতি লাপ্লাসের স্বপ্নের অন্তিম অবস্থারই ইঙ্গিত। অবশ্য আমরা এখনো কল্পনা করতে পারি কোনো এক কোন এক অতিপ্রাকৃত জীব সাপেক্ষ এমন একগুচ্ছ বিধি রয়েছে যে বিধি ঘটনাবলী সম্পূর্ণভাবে নির্ধারণ করে। তিনি হয়তো কোনরকম অস্থিরতা সৃষ্টি না করেই মহাবিশ্বের বর্তমান অবস্থা পর্যবেক্ষণ করতে পারেন। কিন্তু আমাদের মত সাধারণ মরণশীল জীবের পক্ষে মহাবিশ্বের সেই প্রতিরূপের কোনো আকর্ষণ নেই। তার চাইতে বরং ওকামস রেজর (Occam’s razor) নামক মিতব্যয়িতার নীতি প্রয়োগ করে তত্ত্বটির যা কিছু পর্যবেক্ষণ করা যায় না সবটাই ছেঁটে বাদ দিতে পারি। ঊনিশশ কুড়ির দশকে এই দৃষ্টিভঙ্গির সাহায্যে হাইজেনবার্গ, এরভিন শ্রয়েডিংগার এবং পল ডিবাক বলবিদ্যার পুনর্গঠন করে কণাবাদী বলবিদ্যা (quantum mechanics) নামক নতুন তত্ত্ব প্রতিষ্ঠা করেন। এই নতুন তত্ত্বের ভিত্তি হল অনিশ্চয়তাবাদ। এই তত্ত্ব অনুসারে কণিকাগুলির আর পৃথক সুসংজ্ঞিত (well-defined) অপর্যবেক্ষণযোগ্য অবস্থান এবং গতিবেগ রইল না। তার বদলে তাদের থাকল কোয়ান্টাম অবস্থা। সে অবস্থা গতিবেগ এবং অবস্থানের সমন্বয়।
সাধারণত, কণবাদী বলবিদ্যার (quantum mechanics) ভবিষ্যদ্বাণীতে একটি পর্যবেক্ষণের একক সুনিশ্চিত ফল থাকে না। তার বদলে সে ভবিষ্যদ্বাণীতে থাকে অনেকগুলি পৃথক পৃথক (different) ফলশ্রুতি। তাছাড়া থাকে ফলগুলির প্রতিটির কতটা সম্ভাব্যতা। অর্থাৎ কেউ যদি বহুসংখ্যক সমরূপতন্ত্রের (similar system) একই মাপ নেন এবং তাদের প্রতিটি যদি একইভাবে শুরু হয়ে থাকে, তাহলে দেখতে পাবেন বিশেষ সংখ্যক ক্ষেত্রে মাপন ফল হবে ক। ভিন্ন আর কিছু ক্ষেত্রে মাপন ফল হবে খ এবং এই রকম (and so on)। কতবার ফল ক কিম্বা খ হবে সে সম্পর্কে একটা আসন্ন (approximate) সংখ্যা ভবিষ্যদ্বাণীতে থাকতে পারে। কিন্তু একক একটি মাপনের বিশেষ ফল (specific result) সম্পর্কে ভবিষ্যদ্বাণী করা যাবে না। সুতরাং কোয়ান্টাম বলবিদ্যা বিজ্ঞানের ক্ষেত্রে উপস্থিত করেছে ভবিষ্যদ্বাণী করার অসম্ভাব্যতা কিম্বা একটা এলোমেলো অনিশ্চিত অবস্থা (randomness)।
১। ওয়ামস রেজরঃ উইলিয়াম অব ওকাম (১২৮৫-১৩৪৯)। ওকামের নামে পরিচিত মিতব্যয়িতার নীতি। এ নীতি গ্যালিলিওর মতো অনেকেই অনুসরণ করেছেন। নীতিটির মূল বক্তব্য হলঃ সরলতম প্রকল্পই গ্রহণযোগ্য – অনুবাদক।
এই পরিস্থিতি এড়ানো অসম্ভব। এই সমস্ত চিন্তাধারার বিকাশে আইনস্টাইন খুব গুরুত্বপূর্ণ ভূমিকা পালন করেছিলেন। কিন্তু এ ব্যাপারে তাঁর খুবই আপত্তি ছিল। কোয়ান্টাম তত্ত্বে অবদানের জন্য আইনস্টাইনকে নোবেল পুরস্কার দেওয়া হয়েছিল। কিন্তু তা সত্ত্বেও মহাবিশ্ব শাসিত হয় আপতন (chance) দ্বারা- এ তত্ত্ব আইনস্টাইন কখনো মেনে নিতে পারেন নি। এ সম্পর্কে তাঁর মনোভাব সংক্ষেপে তাঁর বিখ্যাত প্রতিবেদনে বলা হয়েছে- “ঈশ্বর পাশা খেলেন না।“ কিন্তু অন্যান্য বৈজ্ঞানিকদের অধিকাংশই কোয়ান্টাম বলবিদ্যাকে মেনে নিতে ইচ্ছুক ছিলেন। তার কারণ, এ বলবিদ্যার সঙ্গে পরীক্ষামূলক তথ্যের নিখুঁত ঐক্য ছিল। সত্যিই এ তথ্য বিশেষভাবে সাফল্য লাভ করেছে। আধুনিক বিজ্ঞান এবং প্রযুক্তিবিদ্যার প্রায় অধিকাংশের ভিত্তি এই তত্ত্ব। ট্রানজিস্টার এবং সমকলিত পরিপথ (integrated circuit) নিয়ন্ত্রণ করে এই তত্ত্ব। টেলিভিশন এবং ইলেকট্রনিক যন্ত্রপাতিরও অবিচ্ছেদ্য উপাদান ট্রানজিস্টার এবং সমকলিত পরিপথ (integrated circuit)। আধুনিক রসায়ন এবং জীববিদ্যারও ভিত্তি এই তত্ত্ব। ভৌতবিজ্ঞানের যে দুটি ক্ষেত্রে কোয়ান্টাম বলবিদ্যাকে এখনো সঠিকভাবে যুক্ত করা যায়নি, সে দুটি হ্ল মহাকর্ষ এবং মহাবিশ্বের বৃহৎমাত্রিক গঠন (large scale structure)।
আলোক তরঙ্গ দিয়ে গঠিত হলেও প্ল্যাঙ্কের কোয়ান্টাম প্রকল্প বলে, কোনো
কোনো অবস্থায় আলোকের আচরণ এমন যে মনে হয় আলোক কণিকার দ্বারা গঠিত। আলোক শুধুমাত্র (packet) কিম্বা কোয়ান্টাম রূপেই নির্গত হতে পারে কিম্বা বিশোষিত হতে পারে। একইভাবে হাইজেনবার্গের অনিশ্চয়তাবাদের অর্থ কণিকাও কোনো কোনো ব্যাপারে তরঙ্গের মতো আচরণ করে। তাদের কোন নিশ্চিত অবস্থা নেই। সেগুলি বিশেষ সম্ভাবনায় বিতরিত হয়ে “প্রলিপ্ত হয়” (smeared out with a certain probability distribution)। কোয়ান্টাম গণিতের তত্ত্বের ভিত্তি সম্পূর্ণ অন্য এক ধরণের গণিত। এ গণিত কণিকা এবং তরঙ্গের বাগ্বিধিতে (terms) আর বাস্তব জগতের বিবরণ দান করে না। এই সমস্ত
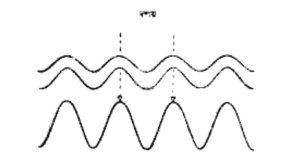
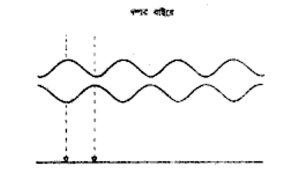
বাগ্বিধিতে শুধুমাত্র পর্যবেক্ষণ করা বিশ্বেরই বিবরণ দেওয়া যেতে পারে। সেজন্য কোয়ান্টাম বলবিদ্যাতে তরঙ্গ এবং কণিকার ভিতরে দ্বিত্ব (duality) রয়েছে। কোনো কোনো উদ্দেশ্যে কণিকাগুলিকে তরঙ্গরূপে চিন্তা করলে সুবিধা হয়, আবার কোনো কোনো উদ্দেশ্যে তরঙ্গকে কণিকা রূপে চিন্তা করলেই ভাল। এর একটা গুরুত্বপূর্ণ ফলশ্রুতি হল, দুই কেতা (set) তরঙ্গ কিম্বা কণিকার ভিতরে ব্যতিচার (interference) পর্যবেক্ষণ করা সম্ভব। অর্থাৎ এক কেতা (set) তরঙ্গের শীর্ষ অন্য কেতা (set) তরঙ্গপাদের (wave trough) সঙ্গে সমস্থানিক (coincide) হতে পারে। তা হলে দুই কেতা তরঙ্গ পরস্পরকে বাতিল করে দেবে। আশা করা যেতে পারত দুটি যোগের ফলে আরো শক্তিশালী একটা তরঙ্গ হবে কিন্তু সেটা হয় না (চিত্র- ৪.১)। সাবানের ফেনার বুদবুদের ভিতরে যে রং দেখা যায়, সেটা আলোকের ক্ষেত্রে ব্যতিচারের (interference) একটি সুপরিচিত উদাহরণ। যে সূক্ষ্ম জলের পর্দা ঐ বুদবুদটি গঠন করে, তার দুপাশ থেকে আলোর প্রতিফলনই এর কারণ। সাদা আলো বিভিন্ন তরঙ্গদৈর্ঘের আলোক নিয়ে গঠিত। বিশেষ কয়েকটি তরঙ্গদৈর্ঘের ক্ষেত্রে একদিক থেকে প্রতিফলিত তরঙ্গগুলির শীর্ষ অন্য দিক থেকে প্রতিফলিত তরঙ্গপাদ সমস্থানিক (coimcide) হয়। এই তরঙ্গদৈর্ঘের অনুরূপ রংগুলি প্রতিফলিত আলোকে অনুপস্থিত থাকে। সে আলোকগুলিকে রঙ্গিন মনে হয়।
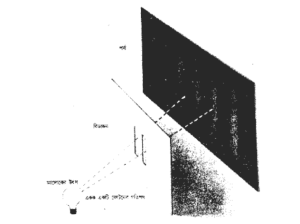
কোয়ান্টাম বলবিদ্যা যে দ্বিত্ব (duality) উপস্থাপন করেছে, তার দরুন কণিকার ক্ষেত্রেও ব্যতিচার হতে পারে। তথাকথিত দুটি চেরা ছিদ্রের পরীক্ষা (two-slit experiment, চিত্র ৪.২) এর একটা বিখ্যাত উদাহরণ। দুটি সমান্তরাল ও সরু চেরাই যুক্ত একটা বিভাজক প্রাচীরের কথা বিবেচনা করুন। প্রাচীরের একপাশে একটা বিশেষ রঙ্গের আলোকের উৎস স্থাপন করা হোক (অর্থাৎ, একটি বিশেষ তরঙ্গদৈর্ঘের আলো)। অধিকাংশ আলোই বিভাজক প্রাচীরে পড়বে কিন্তু খুব সামান্য পরিমাণ আলো ঐ চেরাই করা ফাঁকের ভিতর দিয়ে যাবে। এবার ভেবে নেওয়া যাক বিভাজক প্রাচীরের অন্যদিকে একটা পর্দা টাঙ্গানো হয়েছে। পর্দার যে কোনো বিন্দুতেই দুটি চেরাই করা ফাঁক থেকে তরঙ্গ এসে পড়বে। কিন্তু সাধারণত দুটি চেরাই করা ফাঁক দিয়ে উৎস থেকে পর্দায় পৌঁছাতে আলোর ভিন্ন ভিন্ন দূরত্ব অতিক্রম করতে হবে। এর অর্থ হবে চেরাইয়ের ফাঁক দিয়ে নির্গত তরঙ্গগুলি যখন পর্দায় পৌঁছাবে তখন তারা পরস্পর সাপেক্ষ একই দশায় (phase) থাকবে না। কোনো কোনো ক্ষেত্রে তারা পরস্পরকে বাতিল করবে আবার কোনো কোনো ক্ষেত্রে তারা পরস্পরকে শক্তিশালী করবে। ফল হবে আলোর এবং অন্ধকারের একটা বিশিষ্ট নক্সার ঝালর।
উল্লেখ্যোগ্য ব্যাপার হল, যদি আলোক উৎসের বদলে নির্দিষ্ট নিশ্চিত গতি সম্পন্ন কোনো কণিকা প্রতিস্থাপন করা যায়, তা হলে একই রকম নক্সা পাওয়া যাবে। সে কণিকা ইলেক্ট্রনও হতে পারে (এর অর্থ হল অনুরূপ তরঙ্গগুলিরও একটা নির্দিষ্ট নিশ্চিত দৈর্ঘ্য রয়েছে)। ব্যাপারটা আরো অদ্ভুত এইজন্য যে শুধুমাত্র একটি চেরাই করা ফাঁক থাকলে নক্সা পাওয়া যায় না। পাওয়া যায় পর্দার উপরে সমরূপে বন্টিত (uniformly distributed) ইলেক্ট্রন। অনেকে ভাবতে পারেন, আর একটি চেরাই করা ফাঁক থাকলে পর্দার প্রতিবিন্দুতে যে ইলেক্ট্রনগুলি আঘাত করছে সেগুলির সংখ্যা বাড়বে। কিন্তু ব্যতিচারের (interference) জন্য বাস্তবে কোনো কোনো স্থানে ইলেক্ট্রনের সংখ্যা বরং কমে যায়। এই চেরাই করা ফাঁক দুটো দিয়ে যদি একটি করে ইলেক্ট্রন পাঠানো যায়, তা হলে আশা করা উচিত ছিল ইলেক্ট্রনগুলি কোনো বার একটি ফাঁক দিয়ে ঢুকবে, কোনো বার অন্য ফাঁক দিয়ে ঢুকবে। অর্থাৎ শুধুমাত্র একটি ফাঁক হলে তাদের আচরণ যে রকম হতো, সে রকম আচরণ হবে। ফলে পর্দার উপরে সমরূপ বন্টন হবে। বাস্তব ক্ষেত্রে কিন্তু একটি করে ইলেক্ট্রন পাঠালেও নক্সা দেখা যায়। তা হলে প্রতিটি ইলেক্ট্রন নিশ্চয়ই একই সময়ে দুটি ফাঁক দিয়ে ঢুকছে।
কণিকাগুলির ভিতরে ব্যতিচার (interference) আমাদের পরমাণুর গঠন বোঝার পক্ষে একটি বিনিশ্চায়ক(crucial) পরিঘটনা। রসায়ন ও জীববিদ্যায় এই পরমাণুই মূল একক (basic unit)। আর এই পরমাণুই আমরা ও আমাদের চারপাশে যা আছে সেগুলি গঠন করার ইট। এ শতাব্দীর প্রথমে ভাবা হতো অণুগুলি অনেকটা সূর্যের কক্ষপথে ঘূর্ণায়মান গ্রহের মতো। ইলেক্ট্রনগুলি [অপরা (negative) বৈদ্যুতিক কণিকা] কেন্দ্রীয় নিউক্লিয়াসের চারপাশে কক্ষপথে ঘূর্ণায়মান। কেন্দ্রীয় নিউক্লিয়াস পরা (positive) বিদ্যুৎ বহন করে। অনুমান করা হতো সূর্য এবং গ্রহগুলির অন্তর্বর্তী মহাকর্ষীয় আকর্ষণ (gravitational attraction) যে রকম গ্রহগুলিকে তাদের কক্ষপথে রাখে ঠিক সেই রকম অপরা এবং পরা বিদ্যুতের আকর্ষণও ইলেক্ট্রন গুলিকে তাদের কক্ষপথে রাখে। এ তত্ত্বের অসুবিধা হল, কোয়ান্টাম বলবিদ্যার আগেকার বলবিদ্যা এবং বিদ্যুৎবিজ্ঞানের (electricity) বিধি অনুসারে পূর্বাভাস ছিলঃ ইলেক্ট্রনগুলি ক্রমশ শক্তি হারাবে এবং ক্রমশ ঘুরতে ঘুরতে ভিতরে প্রবেশ করবে এবং নিউক্লিয়াসের সঙ্গে তাদের সংঘর্ষ হবে। এর অর্থ হতো পরমাণু এবং সমস্ত পদার্থই দ্রুত চুপসে অত্যন্ত ঘন একটি অবস্থায় পৌঁছিবে। ১৯১৩ খৃষ্টাব্দে ডেনমার্কের বৈজ্ঞানিক নীলস বোর (Niels Bohr) এই সমস্যার একটি আংশিক সমাধান পেয়েছিলেন। তাঁর প্রস্তাবনা (suggestion) ছিল ইলেকট্রনগুলি হয়তো কেন্দ্রীয় নিউক্লিয়াস থেকে যে কোনো দূরত্বে অবস্থিত কক্ষপথে প্রদক্ষিণ করতে পারে না। প্রদক্ষিন করতে পারে কয়েকটা বিশেষ নির্দিষ্ট দূরত্বে। এছাড়া যদি অনুমান করা যায় এই সমস্ত দূরত্বের যে কোনো একটিতে মাত্র একটি কিম্বা দুটি ইলেকট্রন কক্ষপথে ঘুরতে পারে তাহলে পরমাণু চুপসে যাওয়ার সমস্যা সমাধান করা যেতে পারে। কারণ, সে ক্ষেত্রে সর্বনিম্ন শক্তি এবং দূরত্বে অবস্থিত কক্ষপথ ছাড়া ইলেকট্রনগুলি অন্য কোনো কক্ষপথে ঘুরতে পারে না।
এই প্রতিরূপ সরলতম পরমাণু হাইড্রোজেনের গঠন খুব ভালোই ব্যাখ্যা করতে পারে। কারণ তার নিউক্লিয়াসের চারপাশে কক্ষপথে ঘূর্ণায়মান একটিমাত্র ইলেক্ট্রন থাকে। কিন্তু এই তত্ত্ব কি করে আরো জটিল পরমাণুর ক্ষেত্রে প্রসারিত করা যায় সেটা খুব স্পষ্ট ছিল না। তা ছাড়া অনুমোদিত সীমিত কয়েক কেতা মাত্র কক্ষ সম্পর্কে ধারণা খুব যাদৃচ্ছিক বলে মনে হোত। কোয়ান্টাম বলবিদ্যার নতুন তত্ত্ব এই অসুবিধা দূর করেছে। এই তত্ত্বে প্রকাশ পেয়েছে নিউক্লিয়াসের সর্বদিকে কক্ষপথে ঘূর্ণায়মান ইলেকট্রনকে একটি তরঙ্গও ভাবা চলে। সেই তরঙ্গের দৈর্ঘ্য নির্ভর করবে তার গতিবেগের উপর। কোনো কোনো কক্ষপথের ক্ষেত্রে কক্ষের দৈর্ঘ্য হবে ইলেক্ট্রনের তরঙ্গদৈর্ঘ্যের একটি পূর্ণ সংখ্যার অনুরূপ (তবে ভগ্নাংশের নয়)। এই সমস্ত কক্ষপথের ক্ষেত্রে প্রতি আবর্তনে তরঙ্গশীর্ষ থাকবে একই জায়গায়। সুতরাং তরঙ্গগুলি যোগ হতে থাকবে। এই কক্ষপথগুলি হবে বোরের অনুমোদিত কক্ষগুলির অনুরূপ। কিন্তু যে সমস্ত কক্ষপথের দৈর্ঘ্য তরঙ্গদৈর্ঘ্যগুলির একটি পূর্ণ সংখ্যা নয়, সে সমস্ত ক্ষেত্রে ইলেক্ট্রনগুলি যখন ঘূর্ণায়মান তখন প্রতিটি তরঙ্গশীর্ষকে একটি তরঙ্গপাদ বাতিল করে দেবে। যে তরঙ্গগুইর দৈর্ঘ্য পূর্ণ সংখ্যা নয়, সেগুলি অনুমোদিত হবে না।
আমেরিকান বৈজ্ঞানিক রিচার্ড ফেনম্যানের (Richard Feynman) উপস্থিত করা তথাকথিত ইতিহাসের যোগফল (sum over histories), তরঙ্গ এবং কণার দ্বিত্ব (duality) অনুধাবন করার একটা খুব সুন্দর পদ্ধতি। এই উপস্থাপনে চিরায়ত অ-কোয়ান্টাম তত্ত্বের মতো স্থান-কালে কণিকার একটি মাত্র ইতিহাস কিম্বা পথ অনুমান করা হয় না। তার বদলে অনুমান করা হয় কণিকাটি সম্ভাব্য যে কোনো পথেই ক থেকে খ-তে যেতে পারে। প্রতিটি পথের সঙ্গে দুটি সংখ্যা যুক্ত। একটি সংখ্যা তরঙ্গের আকার নির্দেশক, আর অন্যটি নির্দেশ করে এই চক্রে তার স্থান (অর্থাৎ এতা শীর্ষে না পাদে অবস্থিত)। ক থেকে খ-এ যাবার সম্ভাবনা পাওয়া যায় পথ সাপেক্ষ সমস্ত তরঙ্গের যোগফল দিয়ে। সাধারণভাবে কাছাকাছি পথের কেতাগুলি তুলনা করলে (a set of neighbouring path) এই চক্রে দশা (phase) অথবা অবস্থানের প্রচুর পার্থক্য দেখা যাবে। এর অর্থ হল- এই সমস্ত পথের সঙ্গে সংশ্লিষ্ট তরঙ্গগুলি প্রায় নির্ভুলভাবে একে অপরকে বাতিল করে দেবে। তবে কাছাকাছি পথগুলির কোনো কোনো কেতার (sets) পথগুলির ভিতর দশার (phase) খুব পার্থক্য হবে না। এই পথগুলি সাপেক্ষ তরঙ্গগুলি পরস্পরকে বাতিল করবে না। এই পথগুলি বোরের অনুমোদিত কক্ষপথগুলির অনুরূপ।
এই ধারণাগুলির ভিত্তিতে মূর্ত গাণিতিক গঠনের সাহায্যে আরো জটিল পরমাণুর ক্ষেত্রে, এমন কি, অণুর ক্ষেত্রেও অনুমোদিত কক্ষপথগুলি গণনা করা তুলনায় বেশ সহজ ছিল। অণুগুলি কক্ষস্থিত ইলেক্ট্রন দ্বারা আবদ্ধ একাধিক পরমাণু দ্বারা গঠিত। এই ইলেক্ট্রনগুলি একাধিক কেন্দ্রকে (নিউক্লিয়াস) প্রদক্ষিণ করে। অণুর গঠন এবং তাদের পারস্পারিক প্রতিক্রিয়া সমগ্র রসায়ন শাস্ত্র এবং জীববিদ্যার ভিত্তি। সে জন্য নীতিগতভাবে কোয়ান্টাম বলবিদ্যা আমাদের চারপাশে আমরা যা কিছু দেখি সে সম্পর্কে পূর্বাভাস দেবার সামর্থ্য দান করে। অবশ্য সে সামর্থ্য অনিশ্চয়তাবাদ দিয়ে সীমিত (কার্যক্ষেত্রে কিন্তু যে সমস্ত তন্ত্রে কয়েকটির বেশি ইলেক্ট্রন আছে সেগুলি সম্পর্কে গণনা এত জটিল যে আমরা সে গণনা করতে পারি না)।
মনে হয় আইনস্টাইনের ব্যাপক অপেক্ষবাদ মহাবিশ্বের বৃহৎমাত্রিক গঠনের নিয়ামক। এটা হল তথাকথিত চিরায়ত তত্ত্ব (classical theory), অর্থাৎ এ তত্ত্ব কোয়ান্টাম বলবিদ্যার অনিশ্চয়তাবাদ বিবেচনা করে না। অথচ অন্যান্য তত্ত্বের সঙ্গে সঙ্গতি রক্ষার জন্য এটা বিবেচনা করা উচিত। এর জন্য পর্যবেক্ষণফলের সঙ্গে কোনোরকম গোলমাল না হওয়ার কারণ, সাধারণত আমাদের অভিজ্ঞতায় যে সমস্ত মহাকর্ষীয় ক্ষেত্র আমরা পাই সেগুলি খুবই দুর্বল। ইতিপূর্বে আলোচিত অনন্যতার উপপাদ্য (singularity theorem) অনুসারে কিন্তু মহাকর্ষীয় ক্ষেত্রের অন্তত দুটি পরিস্থিতিতে খুবই শক্তিশালী হওয়া উচিতঃ কৃষ্ণগহ্বর (back hole) এবং বৃহৎ বিস্ফোরণ (big bang)। এর রকম শক্তিশালী ক্ষেত্রগুলিতে কোয়ান্টাম বলবিদ্যার অভিক্রিয়ার গুরুত্ব থাকা উচিত। এক অর্থে চিরায়ত ব্যাপক অপেক্ষবাদ অসীম ঘনত্বের (infinite density) বিন্দু সম্পর্কে ভবিষ্যদ্বাণী করে নিজেরই পতন সম্পর্কে ভবিষ্যদ্বাণী করেছে, ঠিক তেমনি চিরায়ত বলবিদ্যা (অর্থাৎ যে বলবিদ্যা কোয়ান্টাম নয়) পরমাণু চুপসে অসীম ঘনত্ব প্রাপ্ত হবে। এই ভবিষ্যদ্বাণী করে নিজের পতন সম্পর্কে ভবিষ্যদ্বাণী করেছে। ব্যাপক অপেক্ষবাদ এবং কোয়ান্টাম বলবিদ্যাকে ঐক্যবদ্ধ করে এরকম সঙ্গতিপূর্ণ সম্পূর্ণ একটি তত্ত্ব এখনো আমাদের নেই, কিন্তু সে তত্ত্বের অবয়ব কি রকম হবে সে সম্পর্কে আমাদের কিছু কিছু জানা আছে। কৃষ্ণগহ্বর এবং বৃহৎ বিস্ফোরণ সাপেক্ষ এইগুলির ফলশ্রুতি নিয়ে আমরা পরের অধ্যায়গুলিতে আলোচনা করব। আপাতত আমরা ইদানিং প্রকৃতির অন্যান্য বলগুলিকে একক ঐক্যবদ্ধ কোয়ান্টাম তত্ত্বে বুঝবার যে আধুনিক প্রচেষ্টাগুলি হয়েছে, দৃষ্টিপাত করব সেই দিকে।
“কালের সংক্ষিপ্ত ইতিহাস” বই সম্পর্কিত আপনার মন্তব্যঃ